เมื่อขึ้น ม.3 มาน้อง ๆ หลายคนอาจจะได้เจอกับเนื้อหาคณิตศาสตร์ที่เกี่ยวข้องกับพหุนามกันใช่มั้ยครับ ซึ่งสิ่งที่เราต้องทำบ่อย ๆ ในเรื่องพหุนามคือการแยกตัวประกอบของพหุนามเหล่านั้น วันนี้พี่ได้นำสรุปเนื้อหาการแยกตัวประกอบของพหุนามหลาย ๆ แบบมาให้น้อง ๆ ได้อ่านกันครับ จะมีพหุนามแบบได้ ใช้เทคนิคอะไรบ้าง ไปดูเนื้อหากันเลยยย
ความรู้เบื้องต้นเกี่ยวกับพหุนาม
พหุนาม
คือเอกนามพจน์เดียวหรือเอกนามมากกว่า 1 พจน์ที่เขียนในรูปบวกหรือลบกัน เช่น
- 1 + x + x^2
- x^3 – 3x + 1
- 3x^2 + 9
ดีกรีของพหุนาม
มีค่าเท่ากับดีกรีของพจน์ที่ดีกรีสูงสุดในพหุนามนั้น ๆ เช่น x^3 – 3x + 1 มีดีกรีคือ 3
การแยกตัวประกอบพหุนาม
คือการเขียนพหุนามในรูปการคูณกันของพหุนามที่มีดีกรีต่ำกว่าตั้งแต่สองพหุนามขึ้นไป หรือเขียนพหุนามในรูปที่ง่ายกว่า ซึ่งเราจะแบ่งออกเป็น 7 ทักษะดังนี้ครับ
- การจัดกลุ่มและดึงตัวร่วม
- แยกสองวงเล็บ
- กำลังสองสมบูรณ์
- ผลต่างกำลังสอง
- กำลังสองสมบูรณ์ร่วมกับผลต่างกำลังสอง
- ผลบวกและผลต่างกำลังสาม
- กำลังสามสมบูรณ์
เราไปดูทีละหัวข้อกันเลยครับ!
- การจัดกลุ่มและดึงตัวร่วม
หลักการ : หาตัวประกอบร่วมของทุกพจน์แล้วดึงออกมาเขียนในรูปผลคูณ หรือ จับคู่พจน์ของพหุนามแล้วดึงตัวร่วมขั้นแรกก่อน จึงสามารถดึงต่อได้ในขั้นถัดไป
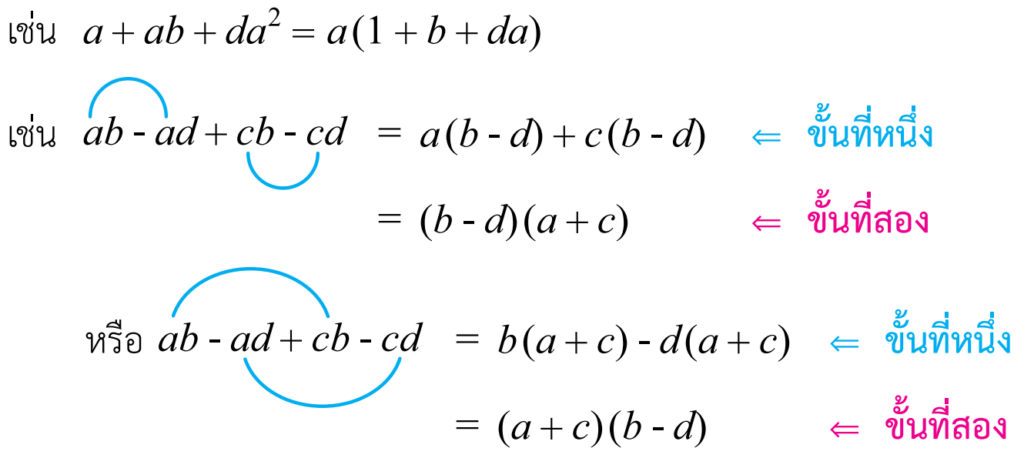
ตัวอย่างที่ 1 จงแยกตัวประกอบของพหุนาม 3x^4y^4 + 6x^2y^2
วิธีทำ
\begin{aligned}3x^4y^4 + 6x^2y^2 &= 3(x^4y^4 + 2x^2y^2) \\&= 3x^2(x^2y^4 + 2y^2) \\&= 3x^2y^2(x^2y^2 + 2)\end{aligned}
ดังนั้น 3x^4y^4 + 6x^2y^2 = 3x^2y^2(x^2y^2 + 2)
- แยกสองวงเล็บ
เรามักจะใช้ทักษะนี้เมื่เราเจอพหุนามอยู่ในรูป Ax^2 + Bx + C สามารถทำได้ดังนี้

ตัวอย่างที่ 2 จงแยกตัวประกอบของพหุนาม 3x^2 – 15x – 18
วิธีทำ
\begin{aligned}3x^2 – 15x – 18 &= 3(x^2 – 5x – 6) \\&= 3[(x)(x) – 5x – (6)(1)] \\&= 3[(x+1)(x-6)] \\&= 3(x+1)(x-6)\end{aligned}
ดังนั้น 3x^2 – 15x – 18 = 3(x+1)(x-6)
- กำลังสองสมบูรณ์
หลักการ : วิธีทำคล้ายกับทักษะก่อนหน้านี้เลยครับ แต่ในทักษะนี้ เราจำเป็นจะต้องรู้เอกลักษณ์การแยกตัวประกอบสองข้อดังนี้ครับ
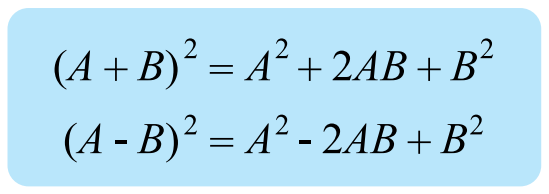
ตัวอย่างที่ 3 จงแยกตัวประกอบของพหุนาม 36y^2 – 60y + 25
วิธีทำ
\begin{aligned}36y^2 – 60y + 25 &= (6y)^2 – 2(6y)(5) + 5^2 \\&= (6y-5)^2\end{aligned}
ดังนั้น 36y^2 – 60y + 25 = (6y-5)^2
- ผลต่างกำลังสอง
หลักการ : แยกตัวประกอบโดยอยู่ในรูปของ
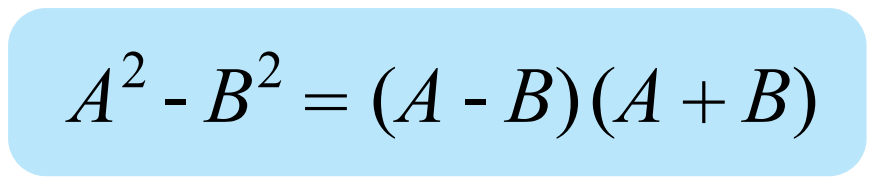
ตัวอย่างที่ 4 จงแยกตัวประกอบของพหุนาม (x+1)^2 – (2x-3)^2
วิธีทำ
\begin{aligned}(x+1)^2 – (2x-3)^2 &= [(x+1) – (2x-3)][(x+1) + (2x-3)] \\&= [x+1 – 2x + 3][x+1 + 2x-3] \\&= (-x+4)(3x-2)\end{aligned}
ดังนั้น (x+1)^2 – (2x-3)^2 = (-x+4)(3x-2)
- กำลังสองสมบูรณ์ร่วมกับผลต่างกำลังสอง
พี่ขออธิบายทักษะนี้ผ่านตัวอย่างง่าย ๆ ดังนี้ครับ

ตัวอย่างที่ 5 จงแยกตัวประกอบของพหุนาม x^2 + y^2
วิธีทำ
\begin{aligned}x^2 + y^2 &= x^2 + 2xy + y^2 – 2xy \\&= (x+y)^2 – 2xy \\&= (x+y)^2 – \sqrt{2xy}^2 \\&= [(x+y) – \sqrt{2xy}][(x+y) + \sqrt{2xy}]\end{aligned}
ดังนั้น x^2 + y^2 = [(x+y) – \sqrt{2xy}][(x+y) + \sqrt{2xy}]
- ผลบวกและผลต่างกำลังสาม
เราจำเป็นจะต้องรู้เอกลักษณ์การแยกตัวประกอบสองข้อดังนี้ครับ
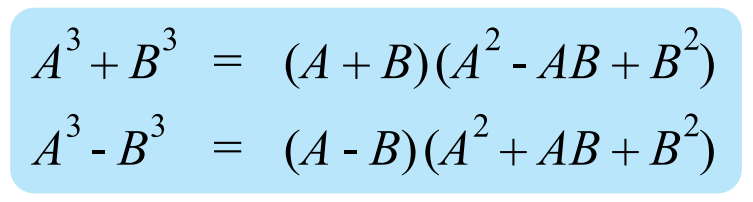
ตัวอย่างที่ 6 จงแยกตัวประกอบของพหุนาม 8x^3 + 64y^3
วิธีทำ
\begin{aligned}8x^3 + 64y^3 &= 2^3x^3 + 4^3y^3 \\&= (2x)^3 + (4y)^3 \\&= (2x+4y)(4x^2 – 8xy + 16y^2) \\&= 2(x+2y)4(x^2 – 2xy + 4y^2) \\&= 8(x+2y)(x^2 – 2xy + 4y^2)\end{aligned}
ดังนั้น 8x^3 + 64y^3 = 8(x+2y)(x^2 – 2xy + 4y^2)
- กำลังสามสมบูรณ์
เราจำเป็นจะต้องรู้เอกลักษณ์การแยกตัวประกอบสองข้อดังนี้ครับ
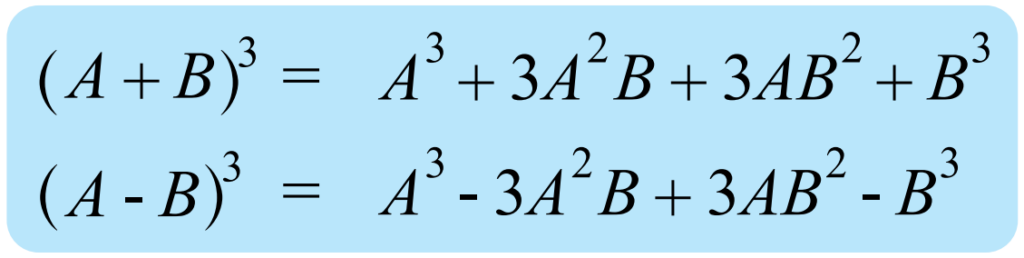
ตัวอย่างที่ 7 จงแยกตัวประกอบของพหุนาม 8x^3 + 6xy^2 + 12x^2y + y^3
วิธีทำ
\begin{aligned}8x^3 + 6xy^2 + 12x^2y + y^3 &= 8x^3 + 12x^2y + 6xy^2 + y^3 \\&= (2x)^3 + 3(2x)^2y + 3(2x)y^2 + y^3 \\&= (2x+y)^3\end{aligned}
ดังนั้น 8x^3 + 6xy^2 + 12x^2y + y^3 = (2x+y)^3
เป็นยังไงกันบ้างครับ สำหรับเนื้อหาเรื่องการแยกตัวประกอบพหุนามที่พี่นำมาฝากน้อง ๆ ทุกคนในวันนี้ น้อง ๆ หลายคนอาจจะอ่านแล้วยังไม่เข้าใจในทันที แต่เราไม่จำเป็นต้องเข้าใจเนื้อหาทั้งหมดนี้ภายในวันเดียวหรือการอ่านเพียงรอบเดียวก็ได้ครับ เราสามารถค่อย ๆ ทบทวนเนื้อหาไปพร้อมกับการฝึกทำโจทย์เพื่อให้เก่งขึ้นได้
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand