สวัสดีน้อง ๆ ทุกคนครับ วันนี้พี่ได้นำสรุปเนื้อหาที่สำคัญมากในวิชาคณิตศาสตร์มาฝากน้อง ๆ กันครับ นั่นก็คือเรื่อง “พาราโบลา” นั่นเองงง สำหรับพาราโบลานั้นนับว่าเป็นเนื้อหาที่สำคัญมาก เพราะน้อง ๆ จะเริ่มได้เจอกันตั้งแต่ ม.ต้น ยาวไปจนถึง ม.ปลาย เลย ถ้าน้อง ๆ พร้อมแล้ว ไปดูกันที่เนื้อหาเลยครับบ
พาราโบลาคืออะไร
พาราโบลา โดยนิยามแล้วหมายถึงเซตของจุดทุกจุดบนระนาบ ซึ่งอยู่ห่างจากจุดคงที่จุดหนึ่ง (จุดโฟกัส) และอยู่ห่างจากเส้นตรงคงที่เส้นหนึ่ง (เส้นไดเรกตริกซ์) เป็นระยะทางเท่ากันเสมอ แน่นอนว่าใครอ่านนิยามของพาราโบลาอันนี้ครั้งแรกก็ต้องไม่เข้าใจแน่นอนว่าคำแต่ละคำมันหมายถึงอะไรกันแน่ใช่มั้ยครับ ถ้าอย่างนั้นให้น้อง ๆ นึกภาพเวลาเราเล่นบาสเกตบอล ในขณะที่เราโยนลูกบอลขึ้นไปในอากาศ เส้นทางที่ลูกบอลเคลื่อนที่ไปนั่นแหละครับคือพาราโบลา โดยพาราโบลาจะมีส่วนประกอบที่สำคัญ ๆ ตามรูปต่อไปนี้เลยย
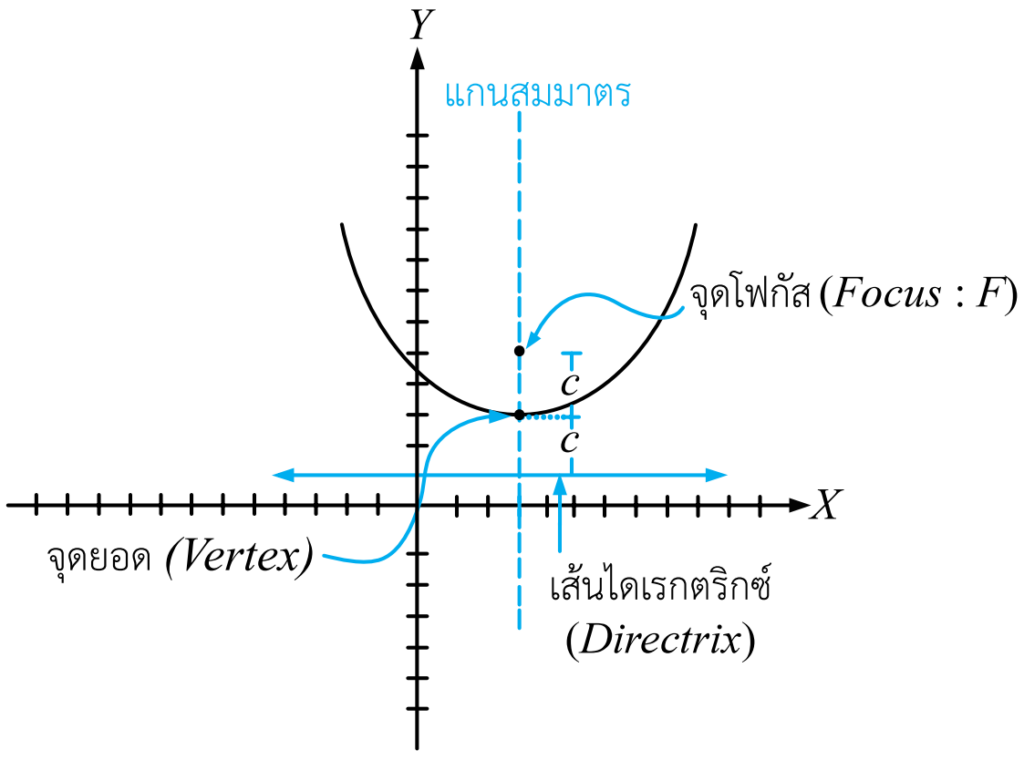
โบลานั้นจะมีสมการคือ y = ax^2 + bx + c เมื่อ a, b, c เป็นค่าคงตัว และ a \ neq 0 นั่นเองครับ และเราอาจเรียกสมการดังกล่าวว่าเป็นฟังก์ชันกำลังสองก็ได้เช่นกันครับ
ลักษณะของพาราโบลา
สำหรับพาราโบลาในระดับ ม.ต้น ที่เราจะได้เจอนั้นจะมีอยู่ทั้งหมด 2 แบบครับ คือ พาราโบลาหงาย และ พาราโบลาคว่ำ โดยถ้า a > 0 กราฟที่ได้จะเป็นพาราโบลาหงาย แต่ถ้า a < 0 กราฟที่ได้จะเป็นพาราโบลาคว่ำนั่นเองครับ น้อง ๆ ดูรูปด้านล่างนี้ได้เลยย
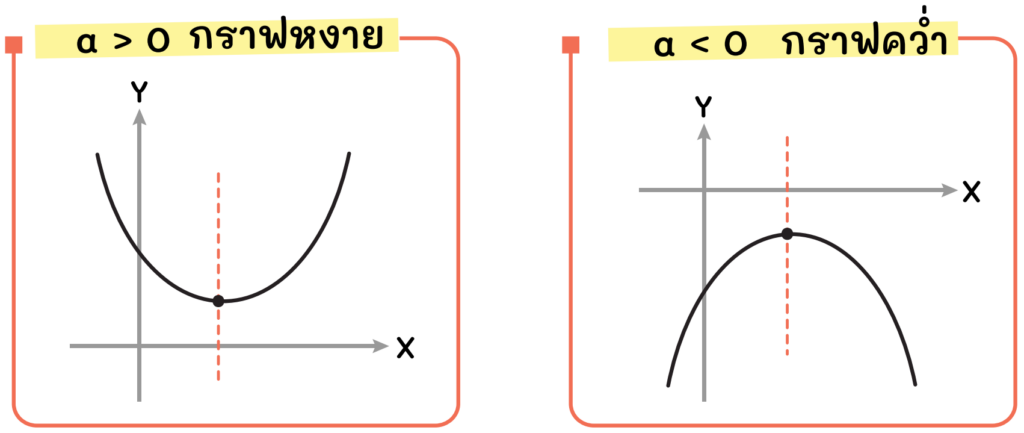
สมการพาราโบลา
ก่อนหน้านี้พี่บอกน้อง ๆ ไปว่าพาราโบลาจะมีสมการในรูปแบบ y = ax^2 + bx + c จริง ๆ แล้วเราสามารถเขียนสมการพาราโบลาได้อีกรูปแบบหนึ่งครับ นั่นก็คือ y = a(x-h)^2 + k เมื่อ a, h, k เป็นค่าคงตัว และ a \ neq 0 โดยการเขียนสมการพาราโบลาทั้งสองแบบนี้มีชื่อเรียกด้วยครับ
- สมการในรูป y = ax^2 + bx + c เรียกว่าสมการรูปทั่วไป
- สมการในรูป y = a(x-h)^2 + k เรียกว่าสมการรูปมาตรฐาน
โดยสมการทั้งสองแบบจะยึดหลักเหมือนกันคือถ้า a > 0 กราฟที่ได้จะเป็นพาราโบลาหงาย แต่ถ้า a < 0 กราฟที่ได้จะเป็นพาราโบลาคว่ำนั่นเองครับ
สมการพาราโบลากับส่วนประกอบของพาราโบลา
พี่ขอนำสมการพาราโบลารูปมาตรฐานกลับมาอีกครั้งนะครับ
y = a(x-h)^2 + k
สมการรูปมาตรฐานนี้บอกข้อมูลเกี่ยวกับพาราโบลาเราหลายอย่างเลยครับ
- ตัวแปร a จะเป็นตัวบอกว่าพาราโบลานั้นกว้างหรือแคบเท่าไหร่
- ตัวแปร h จะเป็นตัวบอกว่าพาราโบลานี้มีจุดยอดอยู่ตรงไหนของแกน X และทำให้เรารู้ด้วยว่าแกนสมมาตรคือเส้นตรง x = h
- ตัวแปร k จะเป็นตัวบอกว่าพาราโบลานี้มีจุดยอดอยู่ตรงไหนของแกน Y
ในระดับ ม.ต้น นั้นพี่อยากให้น้อง ๆ โฟกัสที่ตัวแปร h, k เป็นหลักครับ เพราะเราจะยังไม่ได้ทำอะไรมากกับตัวแปร a
โดยปกติแล้ว โจทย์ที่น้อง ๆ จะได้เจอนั้นเค้ามักจะให้สมการพาราโบลามาในรูปทั่วไป แต่สมการพาราโบลารูปทั่วไปนั้นไม่ได้บอกข้อมูลอะไรกับเราเท่าไหร่ครับ ดังนั้นสิ่งที่เราต้องทำคือพยายามจัดรูปสมการรูปทั่วไปให้อยู่ในรูปมาตรฐานให้ได้ครับ โดยวิธีการจัดรูปนั้นเราจะใช้ความรู้เรื่องกำลังสองสมบูรณ์มาช่วยนั่นเอง
Note : จุดยอดของพาราโบลาหงายคือจุดต่ำสุด และจุดยอดของพาราโบลาคว่ำคือจุดสูงสุด
เพื่อเป็นการฝึกการจัดรูป เรามาลองทำโจทย์เกี่ยวกับการจัดรูปกันสัก 2 ข้อนะครับ
ตัวอย่างที่ 1 จงเขียนสมการพาราโบลา y = x^2 + 2x + 1 ให้อยู่ในรูปทั่วไป
วิธีทำ
\begin{aligned}y &= x^2 + 2x + 1 \\&= x^2 + 2(x)(1) + 1^2 \\&= (x+1)^2 \\&= 1 \cdot (x+1)^2 + 0\end{aligned}
ต่อไปมาดูตัวอย่างที่ยากขึ้นนะครับ
ตัวอย่างที่ 2 จงเขียนสมการพาราโบลา y = 3x^2 + 4x + 7 ให้อยู่ในรูปมาตรฐาน
วิธีทำ
\begin{aligned}y &= 3x^2 + 4x + 7 \\y &= 3\left(x^2 + \dfrac{4}{3}x\right) + 7 \\y &= 3\left(x^2 + (2)(x)\left(\dfrac{2}{3}\right) + \left(\dfrac{2}{3}\right)^2\right) + 7 -3\left(\dfrac{2}{3}\right)^2 \\y &= 3\left(x + \dfrac{2}{3}\right)^2 + \dfrac{17}{3} \\\end{aligned}
การเขียนกราฟพาราโบลา
การเขียนกราฟพาราโบลานั้นเราจำเป็นจะต้องมีสมการของพาราโบลาในรูปมาตรฐาน เพราะว่าสมการในรูปมาตรฐานจะเป็นตัวบอกข้อมูลของพาราโบลานั้น ๆ ให้เราทราบนั่นเองครับ
มาลองทำโจทย์กันเลยครับ
ตัวอย่างที่ 3 จงเขียนกราฟของพาราโบลา y = (x-3)^2 + 2
วิธีทำ
จากสมการที่โจทย์กำหนดให้ เราจะได้ว่า
- พาราโบลานี้เป็นพาราโบลาหงาย
- มีจุดยอดเป็นจุดต่ำสุด
- มีจุดยอดอยู่ที่จุด (3, 2)
- มีเส้นตรง x = 3 เป็นแกนสมมาตร
- ตัดแกน Y (x เป็น 0) ที่จุด (0, 11)
ดังนั้นเราจะเขียนกราฟได้ดังนี้
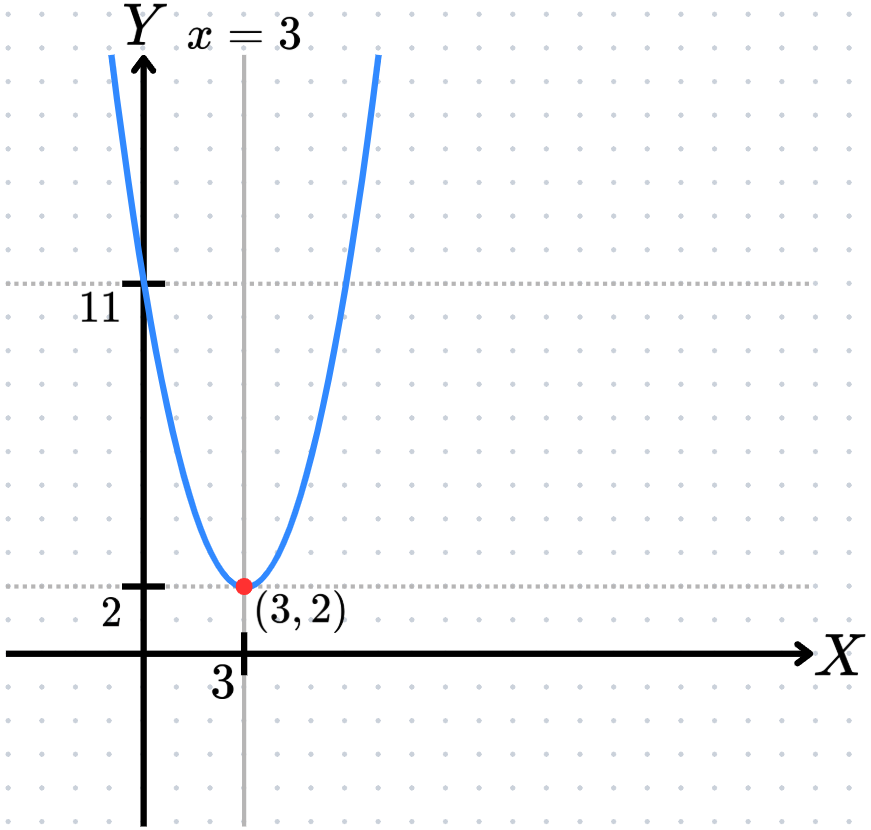
การหาจุดยอดของพาราโบลา
ในบางครั้งเราต้องการทราบว่าจุดยอดของพาราโบลาอยู่ที่จุดไหน แต่การที่เราจะจัดรูปสมการให้เป็นรูปมาตรฐานก็อาจจะใช้เวลามากเกินไปใช่มั้ยครับ ดังนั้นพี่ขอนำเสนออีกวิธีการหนึ่งในการหาจุดยอดของพาราโบลาดังนี้ครับ
วิธีการนี้จะหาจุดยอดได้จากสมการรูปทั่วไปได้เลย นั่นคือ ถ้าเรามีสมการพาราโบลาในรูป y = ax^2 + bx + c เราจะทราบได้ทันทีเลยว่าจุดยอดของมันคือ (h, k) = \left(-\dfrac{b}{2a}, \dfrac{4ac-b^2}{4a}\right)
เมื่อรู้แบบนี้แล้ว ลองไปทำโจทย์กันเลยครับบ
ตัวอย่างที่ 4 จงหาจุดยอดของพาราโบลา y = -0.5x^2 + 7x + 14
วิธีทำ
จากสมการที่โจทย์ให้มา เราจะได้ว่า a = -0.5, b = 7, c = 14
ดังนั้นเราจะได้ว่าจุดยอดของพาราโบลานี้คือ
\begin{aligned}\left(-\dfrac{b}{2a}, \dfrac{4ac-b^2}{4a}\right)&= \left(-\dfrac{7}{2(-0.5)}, \dfrac{4(-0.5)(14)-7^2}{4(-0.5)}\right) \\&= \left(-\dfrac{7}{-1}, \dfrac{-2(14)-49}{-2}\right) \\&= \left(-\dfrac{7}{-1}, \dfrac{-28-49}{-2}\right) \\&= \left(-\dfrac{7}{-1}, \dfrac{-77}{-2}\right) \\&= \left(7, 38.5\right)\end{aligned}
เราจึงสรุปได้ว่าจุดยอดของพาราโบลานี้คือ \left(7, 38.5\right) นั่นเองครับ
ความแตกต่างระหว่างพาราโบลา ม.ต้น และ ม.ปลาย
เนื้อหาของพาราโบลาใน ม.ต้น นั้นจะมีพาราโบลาเพียงแค่ 2 รูปแบบเท่านั้น คือพาราโบลาคว่ำ และพาราโบลาหงาย แต่ในระดับ ม.ปลาย เราจะได้เจอกับพาราโบลาอีก 2 แบบคือพาราโบลาเปิดซ้าย และพาราโบลาเปิดขวา อีกทั้งเรายังจะได้รู้ส่วนประกอบของพาราโบลาเพิ่มขึ้นอีกด้วย เช่น เส้นไดเรกตริกซ์ เลตัสเรกตัม การหาจุดโฟกัส พวกนี้เป็นต้นครับ
เป็นยังไงกันบ้างครับน้อง ๆ กับเนื้อหาและโจทย์ซ้อมมือเรื่องพาราโบลาที่พี่ได้นำมาฝากในวันนี้ อาจจะมีการจัดรูปสมการหรือการมองรูปที่ค่อนข้างท้าทายไปบ้าง แต่พี่เชื่อว่าหากน้อง ๆ ฝึกทำโจทย์บ่อย ๆ เนื้อหาเหล่านี้จะไม่ใช่เรื่องยากเกินความสามารถพวกเราแน่นอนน
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand