สรุปเนื้อหา การเคลื่อนที่วิถีโค้ง ม.4

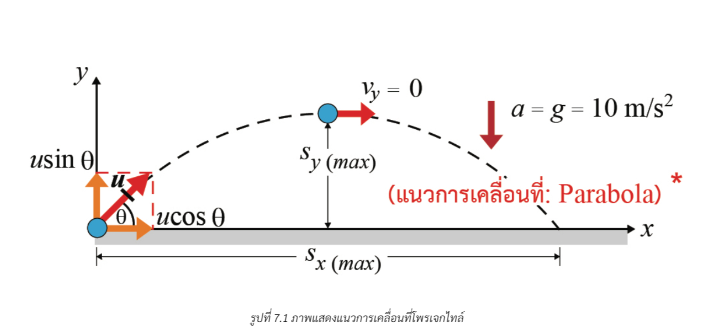
หากผู้สังเกต อยู่ในมุมมองด้านข้างจะเห็นแนวการเคลื่อนที่เป็นโค้งพาราโบล่าดังรูปที่ 7.1

สูตรและการคำนวณ

โพรเจกไทล์ (Projectile) รากศัพท์มาจากคำว่า Project ที่แปลว่าเงา เนื่องจากวัตถุมีการเคลื่อนที่ใน 2 มิติ ซึ่งมีทั้งที่ตั้งฉากและขนานกับแรงโน้มถ่วง ทำให้คำนวณได้ยาก เราจึงทำการฉายเงาในทิศตั้งฉากและขนานกับแนวแรงโน้มถ่วง

เราจะพบว่าในแนวตั้งฉากกับแรงโน้มถ่วงหรือแนวราบนั้น จะไม่มีแรงภายนอกมากกระทำ

\Sigma F = 0 \ \mathrm{N}

นั้นคือ ความเร่งมีค่าเป็นศูนย์

ดังนั้น วัตถุจะเคลื่อนที่ด้วยความเร็วคงที่

เมื่อทำการแตกองค์ประกอบของความเร็วต้นเข้าในแนวราบแล้วนั้นจะได้ว่า

u_{x} = u \cos \theta

เมื่อกำหนดให้

u คือ ความเร็วต้นของวัตถุ

u_{x} คือ องค์ประกอบของความเร็วต้นในแนวราบ

\theta คือ มุมที่ความเร็วต้นทำกับแนวราบ

การกระจัดของวัตถุเคลื่อนที่ได้ตามแนวราบนั้นจะเป็นไปตามสมการ

\begin{aligned} S_{x(t)} &= u_{x(t)} \\ S_{x(t)} &= u \cos \theta t \end{aligned}

เมื่อกำหนดให้

t คือ เวลานับจากวัตถุเริ่มเคลื่อนที่

S_{x(t)} คือการกระจัดในแนวราบที่เวลา t ใดๆ

และเราจะพบว่าในแนวขนานกับแรงโน้มถ่วงหรือในแนวดิ่งนั้น วัตถุจะเคลื่อนที่อิสระภายใต้แรงโน้มถ่วง

\begin{aligned} \Sigma F &= ma \\ mg &=ma \\ a&=g \end{aligned}

นั้นคือ วัตถุจะเคลื่อนที่ภายใต้ความเร่งเนื่องจากสนามโน้มถ่วง

เมื่อทำการแตกองค์ประกอบของความเร็วต้นเข้าในแนวดิ่งแล้วนั้นจะได้ว่า

u_{y} = u\sin \theta

เมื่อกำหนดให้

u_{y}

คือองค์ประกอบของความเร็วต้นในแนวดิ่ง

การกระจัดของวัตถุเคลื่อนที่ได้ตามแนวดิ่งนั้นจะเป็นไปตามสมการ

\begin{aligned} S_{y(t)} &= u_{yt}-\dfrac{1}{2}gt^{2} \\ S_{y(t)} &= u \sin \theta t  –  \dfrac{1}{2}gt^{2} \end{aligned}

เมื่อกำหนดให้

S_{y(t)} คือการกระจัดในแนวดิ่งที่เวลา t ใดๆ

และองค์ประกอบความเร็วในแนวดิ่งที่วินาทีใดๆ จะเป็นไปตามสมการ

v_{y(t)} = u_{y} – gt

เมื่อกำหนดให้

v_{y(t)} คือ องค์ประกอบความเร็วในแนวดิ่งที่เวลา t ใดๆ

ข้อสังเกตุ

ในการคำนวณทั้งสองแนว จะอยู่ภายใต้เวลา t เดียวกันเพราะเกิดจาก เงาของวัตถุเดียวกันนั้นเอง