กดดูรายละเอียดเนื้อหาย่อย
เมื่อพูดถึงเวกเตอร์ น้อง ๆ หลายคนอาจจะคุ้น ๆ กับคำนี้จากเนื้อหาในวิชาฟิสิกส์ใช่ไหมครับ แต่น้อง ๆ รู้มั้ยครับว่าเนื้อหาเรื่องเวกเตอร์นั้นเราจะได้เรียนในวิชาคณิตศาสตร์ ม.ปลาย กันด้วยนะ และพี่ก็ได้สรุปเนื้อหาเหล่านั้นมาให้พวกเราได้อ่านกันแล้วในบทความนี้ครับ ถ้าพร้อมแล้วก็ไปลุยกันเลยยย
✨เวกเตอร์ คือ อะไร
เวกเตอร์ คือ ปริมาณชนิดหนึ่งที่มีทั้งขนาดและทิศทาง เพราะว่ามีปริมาณบางอย่างบนโลกนี้ที่เราไม่สามารถอธิบายเค้าได้โดยบอกแค่ขนาดหรือทิศทางเพียงอย่างเดียว จำเป็นจะต้องบอกทั้งสองอย่างพร้อมกัน เช่น ถ้ามีนักท่องเที่ยวมาถามทางน้อง ๆ ว่าร้านสะดวกซื้อไปทางไหน แน่นอนว่าคำตอบที่เราจะตอบนักท่องเที่ยวไปนั้นจะต้องมีการบอกทั้งทิศทาง ว่าเดินไปทางไหน และบอกระยะทางแบบคร่าว ๆ ด้วยว่าประมาณกี่เมตร ใกล้หรือไกลเท่าไหร่ เป็นต้นครับ
ปริมาณที่เป็นปริมาณเวกเตอร์นั้นมีอยู่มากมายครับ น้อง ๆ บางคนอาจจะคุ้น ๆ มาจากวิชาฟิสิกส์ว่า “แรง” เป็นเวกเตอร์ ใช่แล้วครับ แรงทุกชนิดนั้นเป็นเวกเตอร์ เช่น แรงโนมถ่วงของโลก แรงเสียดทาน แรงตึงเชือก เป็นต้น แต่การบอกว่าเวกเตอร์คือปริมาณที่มีทั้งขนาดและทิศทางโดยการพูดลอย ๆ นั้นอาจจะเป็นนามธรรมเกินไปซักหน่อย เราเลยจะมีการเขียนเพื่อแสดงถึงปริมาณเวกเตอร์ครับ เวลาคุยกันถึงเวกเตอร์จะได้เข้าใจได้ทันทีเลยว่าการเขียนแบบนี้คือเรากำลังพูดถึงเวกเตอร์นั่นเอง โดยการเขียนนั้นเราจะเขียนส่วนของเส้นตรงขึ้นมาเส้นนึง แล้วตามด้วยหัวลูกศร โดยด้านที่ไม่มีหัวลูกศร เราจะให้มันเป็นจุดเริ่มต้นของเวกเตอร์ และด้านที่มีหัวลูกศร เราจะให้มันเป็นจุดสิ้นสุดของเวกเตอร์ครับ ตามรูปต่อไปนี้เลย
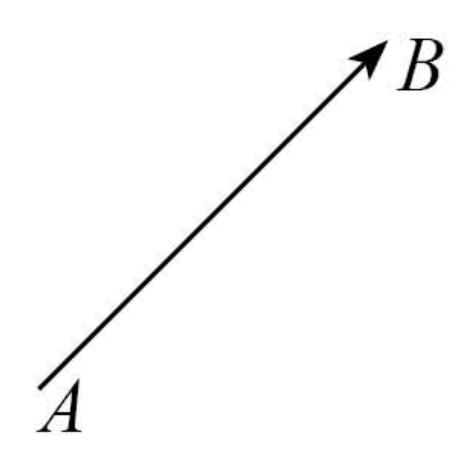
โดยการเขียนเวกเตอร์เราสามารถเขียนได้สองแบบครับ แบบแรกคือเขียนทั้งจุดเริ่มต้น และจุดสิ้นสุดของเวกเตอร์นั้นแล้วตามด้วยการเขียนลูกศรบนหัวด้วย เช่น \vec{AB} แบบที่สองคือการตั้งชื่อขึ้นมาใหม่เป็นตัวอักษรตัวเดียวไปเลยก็ทำได้เช่นกันครับ เช่น \vec{u}
✨ลักษณะของเวกเตอร์
หากเรามีเวกเตอร์อยู่สองเวกเตอร์คือ \vec{u}, \vec{v} ลักษณะสำคัญ ๆ ที่อาจจะเกิดขึ้นได้กับเวกเตอร์ทั้งสองนี้ก็จะมีดังนี้ครับ
✨เวกเตอร์เท่ากัน
เราจะกล่าวว่า \vec{u} เท่ากับ \vec{v} ก็ต่อเมื่อ \vec{u} และ \vec{v} มีขนาดเท่ากันและทิศทางเดียวกันดังรูปครับ
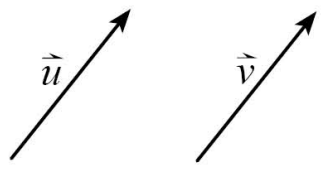
✨เวกเตอร์ขนานกัน
เราจะกล่าวว่า \vec{u} ขนานกับ \vec{v} ก็ต่อเมื่อ \vec{u} และ \vec{v} มีทิศเดียวกันหรือขนานกันดังรูปครับ
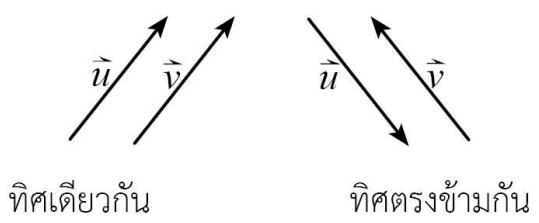
✨นิเสธของเวกเตอร์
นิเสธของ \vec{u} คือเวกเตอร์ที่มีขนาดเท่ากับ \vec{u} แต่มีทิศตรงข้ามกับ \vec{u} และเราจะใช้ -\vec{u} เพื่อแทนนิเสธของ \vec{u} ครับ
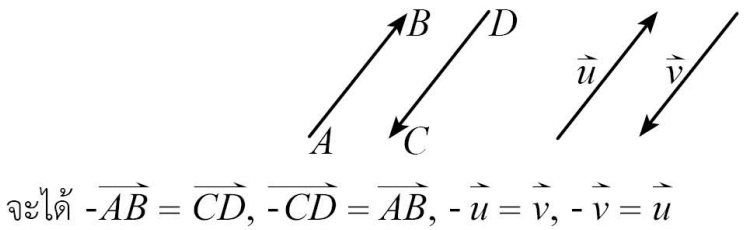
✨การบวกเวกเตอร์
ทำได้โดยการนำหัวของเวกเตอร์นึงไปต่อที่หางของอีกเวกเตอร์นึง แล้วเวกเตอร์ผลลัพธ์ที่ได้จะเป็นเวกเตอร์ใหม่ที่ลากจากหางของเวกเตอร์แรกไปถึงหัวของเวกเตอร์ที่สอง ดังนี้ครับ
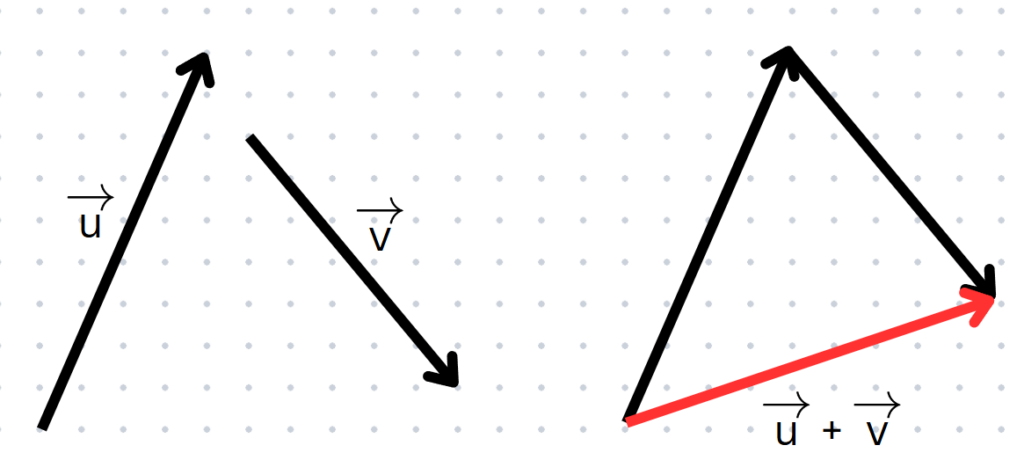
✨การลบเวกเตอร์
สามารถทำได้เหมือนกับการบวกเวกเตอร์ แต่คราวนี้แทนที่เราจะนำเวกเตอร์สองเวกเตอร์มาบวกกันตรง ๆ เราจะบวกด้วยนิเสธของเวกเตอร์ที่นำมาบวกแทนครับ หรือพูดง่าย ๆ ก็คือ ถ้าเราจะหา \vec{u} – \vec{v} เราจะทำได้โดยการมองมันเป็น \vec{u} + (-\vec{v}) นั่นเองครับ
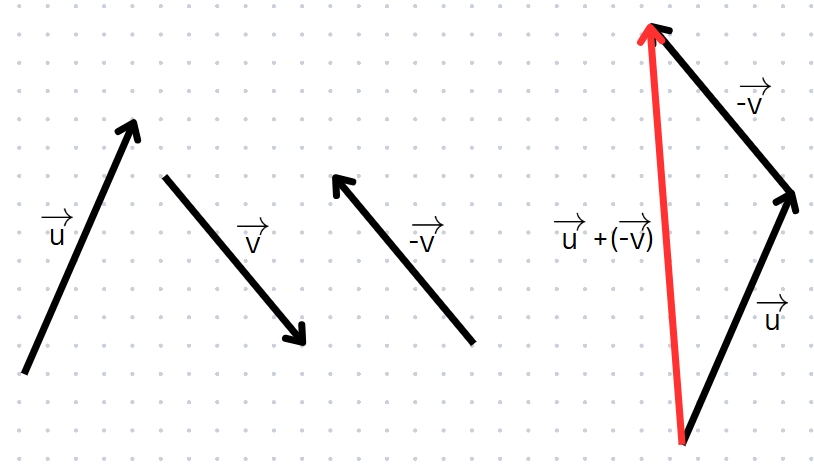
✨เวกเตอร์ศูนย์
คือเวกเตอร์ที่มีขนาดเป็นศูนย์ และเราจะเขียนแทนด้วย \vec{0}
✨สมบัติการบวกของเวกเตอร์
ให้ \vec{u}, \vec{v} และ \vec{w} เป็นเวกเตอร์ใด ๆ จะได้ว่า
- \vec{u} + \vec{v} จะเป็นเวกเตอร์เสมอ นั่นคือเวกเตอร์มีสมบัติปิดการบวก
- \vec{u} + \vec{v} = \vec{v} + \vec{u} นั่นคือเวกเตอร์มีสมบัติสลับที่การบวก
- \vec{u} + (\vec{v} + \vec{w}) = (\vec{u} + \vec{v}) + \vec{w} นั่นคือเวกเตอร์มีสมบัติการเปลี่ยนกลุ่มสำหรับการบวก
- \vec{u} + \vec{0} = \vec{u} = \vec{0} + \vec{u} นั่นคือเวกเตอร์มีเอกลักษณ์การบวก
- \vec{u} + (-\vec{u}) = \vec{0} = (-\vec{u}) + \vec{u} นั่นคือเวกเตอร์มีอินเวอร์สการบวก
✨การคูณเวกเตอร์ด้วยสเกลาร์
ให้ k เป็นจำนวนจริง
ถ้า k > 0 จะได้ว่า k\vec{u} คือเวกเตอร์ที่มีขนาดเป็น k เท่าของเวกเตอร์ \vec{u} และมีทิศเดียวกับเวกเตอร์ \vec{u}
ถ้า k < 0 จะได้ว่า k\vec{u} คือเวกเตอร์ที่มีขนาดเป็น k เท่าของเวกเตอร์ \vec{u} แต่มีทิศตรงข้ามกับเวกเตอร์ \vec{u} เช่น
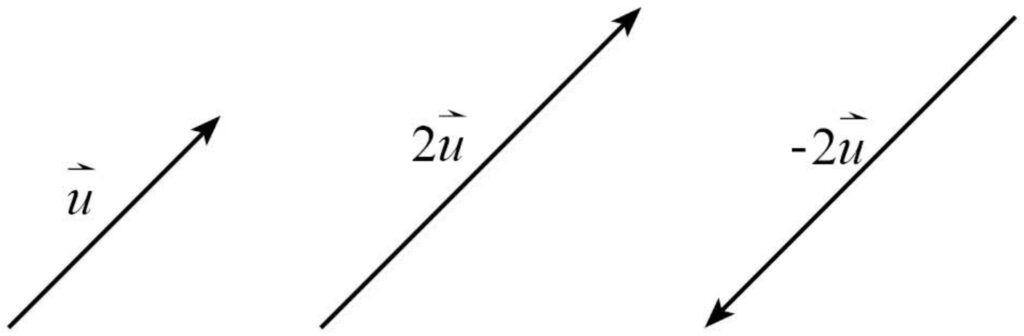
จากรูปน้อง ๆ จะเห็นได้ว่า
2\vec{u} คือเวกเตอร์ที่มีขนาดเป็น 2 เท่าของเวกเตอร์ \vec{u} และมีทิศเดียวกับเวกเตอร์ \vec{u}
-2\vec{u} คือเวกเตอร์ที่มีขนาดเป็น 2 เท่าของเวกเตอร์ \vec{u} แต่มีทิศตรงข้ามกับเวกเตอร์ \vec{u}
✨สมบัติการคูณของเวกเตอร์ด้วยสเกลาร์
ให้ \vec{u}, \vec{v} เป็นเวกเตอร์ใด ๆ และ a, b เป็นจำนวนจริง
- a\vec{u} เป็นเวกเตอร์
- (a+b)\vec{u} = a\vec{u} + b\vec{u}
- a(\vec{u} + \vec{v}) = a\vec{u} + a\vec{v}
- (ab)\vec{u} = a(b\vec{u}) = b(a\vec{u})
- 0\vec{u} = \vec{0}
ถ้า a\vec{u} = \vec{0} จะได้ว่า a = 0 หรือ \vec{u} = \vec{0}
✨เวกเตอร์ในระบบพิกัดฉาก
หลังจากที่เราได้รู้จักเวกเตอร์ สมบัติของเวกเตอร์ และการเขียนเวกเตอร์โดยการใช้ส่วนของเส้นตรงไปแล้ว ต่อไปพี่จะนำเสนออีกวิธีหนึ่งในการเขียนเวกเตอร์ให้น้อง ๆ ดูกันครับ โดยจะเป็นการเขียนเพื่อให้นำไปใช้งานได้สะดวก รวดเร็ว เข้าใจง่าย และบ่งบอกถึงข้อมูลของเวกเตอร์นั้น ๆ ได้ค่อนข้างละเอียด ซึ่งการเขียนเวกเตอร์ดังกล่าวมีอยู่สองแบบให้เราเลือกใช้ดังนี้ครับ
- การเขียนเวกเตอร์ในรูปคอลัมน์เมทริกซ์
จะเป็นการเขียนเวกเตอร์ในรูปของเมทริกซ์ที่มีเพียงหลักเดียว โดยอาจจะมี 2 หรือ 3 แถวก็ได้ขึ้นอยู่กับเวกเตอร์ว่าเวกเตอร์นั้นเป็นเวกเตอร์ 2 หรือ 3 มิติครับ
- การเขียนเวกเตอร์ในรูปของเวกเตอร์ \vec{i}, \vec{j}, \vek{k}
เวกเตอร์ \vec{i}, \vec{j}, \vek{k} คือเวกเตอร์ที่มีขนาดหนึ่งหน่วยและมีทิศทางตามแนวแกน X, Y, Z ตามลำดับ
พี่จะขอใช้ตัวอย่างต่อไปนี้เพื่อแสดงการเขียนให้น้อง ๆ ดูนะครับ
ตัวอย่างที่ 1 จงเขียนเวกเตอร์ \vec{u} ในรูปคอลัมน์เมทริกซ์ และในรูปของเวกเตอร์ \vec{i}, \vec{j}, \vek{k}
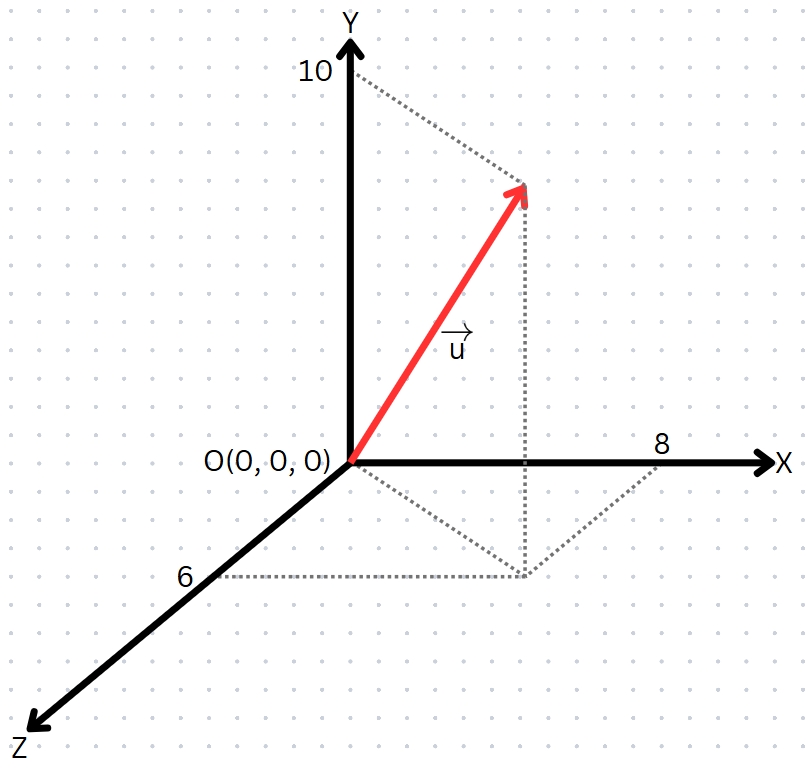
การเขียนในรูปคอลัมน์เมทริกซ์ : \begin{pmatrix} 8 \\ 10 \\ 6 \end{pmatrix}
การเขียนในรูปของเวกเตอร์ \vec{i}, \vec{j}, \vek{k} : 8\vec{i} + 10\vec{j} + 6\vec{k}
✨ขนาดของเวกเตอร์
ถ้า \vec{u} = \begin{pmatrix} a \\ b\end{pmatrix}, \vec{v} = \begin{pmatrix} p \\ q \\ r \end{pmatrix} เราจะได้ว่า
- ขนาดของ \vec{u} = |\vec{u}| = \sqrt{a^2 + b^2}
- ขนาดของ \vec{v} = |\vec{v}| = \sqrt{p^2 + q^2 + r^2}
ตัวอย่างที่ 2 จงหาขนาดของเวกเตอร์ \begin{pmatrix} 8 \\ 10 \\ 6 \end{pmatrix}
วิธีทำ
ขนาดของ \begin{pmatrix} 8 \\ 10 \\ 6 \end{pmatrix} = \sqrt{8^2 + 10^2 + 6^2} = \sqrt{64 + 100 + 36} = \sqrt{200} = 10\sqrt{2} หน่วย
เวกเตอร์หนึ่งหน่วย
เวกเตอร์ 1 หน่วย ทิศเดียวกับ \vec{u} คือ \dfrac{\vec{u}}{|\vec{u}|}
เวกเตอร์ 1 หน่วย ทิศตรงข้ามกับ \vec{u} คือ -\dfrac{\vec{u}}{|\vec{u}|}
เวกเตอร์ 1 หน่วย ขนานกับ \vec{u} คือ \pm\dfrac{\vec{u}}{|\vec{u}|}
เวกเตอร์ k หน่วย ทิศเดียวกับ \vec{u} คือ k\dfrac{\vec{u}}{|\vec{u}|}
เวกเตอร์ k หน่วย ทิศตรงข้ามกับ \vec{u} คือ -k\dfrac{\vec{u}}{|\vec{u}|}
เวกเตอร์ k หน่วย ขนานกับ \vec{u} คือ \pm k\dfrac{\vec{u}}{|\vec{u}|}
✨ผลคูณเชิงสเกลาร์
กำหนดให้ a, b, c, d, e, f เป็นจำนวนจริง และ \vec{u}, \vec{v} เป็นเวกเตอร์ใด ๆ ซึ่ง \vec{u} = a\vec{i} + b\vec{j} + c\vec{k} และ \vec{v} = d\vec{i} + e\vec{j} + f\vec{k} เราจะเรียก \vec{u} \cdot \vec{v} ว่าเป็นผลคูณเชิงสเกลาร์ระหว่าง \vec{u} กับ \vec{v} และ \vec{u} \cdot \vec{v} = ad + be + cf
✨สมบัติของผลคูณเชิงสเกลาร์
- ให้ \vec{u}, \vec{v} \neq \vec{0} เราจะได้ว่า \vec{u} จะตั้งฉากกับ \vec{v} ก็ต่อเมื่อ \vec{u} \cdot \vec{v} = 0
- \vec{u} \cdot \vec{v} = \vec{v} \cdot \vec{u}
- \vec{u} \cdot (\vec{v} \pm \vec{w}) = \vec{u} \cdot \vec{v} \pm \vec{u} \cdot \vec{w}
- m(\vec{u} \cdot \vec{v}) = (m\vec{u}) \cdot \vec{v} = \vec{u} \cdot (m\vec{v})
- \vec{u} \cdot \vec{u} = |\vec{u}|^2
- |\vec{u} + \vec{v}|^2 = |\vec{u}|^2 + 2 \vec{u} \cdot \vec{v} + |\vec{v}|^2
- |\vec{u} – \vec{v}|^2 = |\vec{u}|^2 – 2 \vec{u} \cdot \vec{v} + |\vec{v}|^2
- (\vec{u} + \vec{v}) \cdot (\vec{u} – \vec{v}) = |\vec{u}|^2 – |\vec{v}|^2
- \vec{i} \cdot \vec{i} = \vec{j} \cdot \vec{j} = \vec{k} \cdot \vec{k} = 1
- \vec{i} \cdot \vec{j} = \vec{j} \cdot \vec{k} = \vec{k} \cdot \vec{i} = 0
✨ตัวอย่างที่ 3 กำหนดให้ \vec{u} = -\vec{i} + 2\vec{j} + \vec{k}, \vec{v} = 3\vec{i} + 4\vec{k} จงหา \vec{u} \cdot \vec{v}
วิธีทำ
\begin{aligned}\vec{u} \cdot \vec{v} &= (-\vec{i} + 2\vec{j} + \vec{k}) \cdot (3\vec{i} + 4\vec{k}) \\ &= (-1)(3) + (2)(0) + (1)(4) \\ &= -3 + 0 + 4 \\ &= 1 \end{aligned}
ดังนั้น \vec{u} \cdot \vec{v} = 1
✨ผลคูณเชิงเวกเตอร์
ให้ \vec{u} = \begin{pmatrix} a \\ b \\ c \end{pmatrix}, \vec{v} = \begin{pmatrix} d \\ e \\ f \end{pmatrix} เราจะได้ว่า
\vec{u} \times \vec{v} = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ a & b & c \\ d & e & f \end{vmatrix} = \begin{vmatrix} b & c \\ e & f \end{vmatrix}\vec{i} – \begin{vmatrix} a & c \\ d & f \end{vmatrix}\vec{j} + \begin{vmatrix} a & b \\ d & e \end{vmatrix}\vec{k} และทิศของ \vec{u} \times \vec{v} จะเป็นไปตามรูปต่อไปนี้ครับ
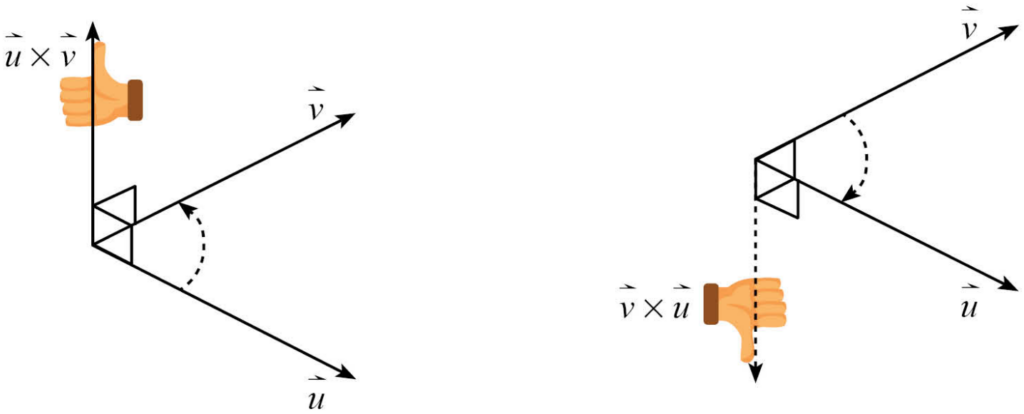
✨สมบัติของผลคูณเชิงเวกเตอร์
กำหนดให้ a, b เป็นจำนวนจริง และ \vec{u}, \vec{v}, \vec{w} เป็นเวกเตอร์ใด ๆ เราจะได้ว่า
- \vec{u} \times \vec{v} = -(\vec{v} \times \vec{u})
- (\vec{u} \pm \vec{v}) \times \vec{w} = \vec{u} \times \vec{w} \pm \vec{v} \times \vec{w}
- \vec{w} \times (\vec{u} \pm \vec{v})= \vec{w} \times \vec{u} \pm \vec{w} \times \vec{v}
- \vec{u} \times (k \vec{v}) = (k \vec{u}) \times \vec{v} = k(\vec{u} \times \vec{v})
- \vec{i} \times \vec{j} = \vec{k}, \vec{j} \times \vec{k} = \vec{i}, \vec{k} \times \vec{i} = \vec{j}
- \vec{u} \times \vec{u} = \vec{0}
✨ตัวอย่างที่ 4 กำหนดให้ \vec{u} = -\vec{i} + 2\vec{j} + \vec{k}, \vec{v} = 3\vec{i} + 4\vec{k} จงหา \vec{u} \times \vec{v}
วิธีทำ
\begin{aligned}\vec{u} \times \vec{v} &= \begin{vmatrix} \vec{i} & \vec{j} &\vec{k} \\ -1 & 2 & 1 \\ 3 & 0 & 4 \end{vmatrix} \\&= \begin{vmatrix} 2 & 1 \\ 0 & 4\end{vmatrix}\vec{i} – \begin{vmatrix} -1 & 1 \\ 3 & 4 \end{vmatrix}\vec{j} +\begin{vmatrix} -1 & 2 \\ 3 & 0 \end{vmatrix}\vec{k} \\&= 8\vec{i} + 7\vec{j} – 6\vec{k} \\ \end{aligned}
ดังนั้น \vec{u} \times \vec{v} = 8\vec{i} + 7\vec{j} – 6\vec{k}
✨การหาพื้นที่และปริมาตร
ในหัวข้อนี้เราจะนำความรู้เรื่องเวกเตอร์มาใช้ในการหาพื้นที่ของรูปสี่เหลี่ยมด้านขนานและปริมาตรของทรงสี่เหลี่ยมด้านขนานกันครับ
การใช้เวกเตอร์ในการหาพื้นที่รูปสี่เหลี่ยมด้านขนาน
กำหนดให้ \vec{u}, \vec{v} เป็นเวกเตอร์ใด ๆ เราจะได้ว่า
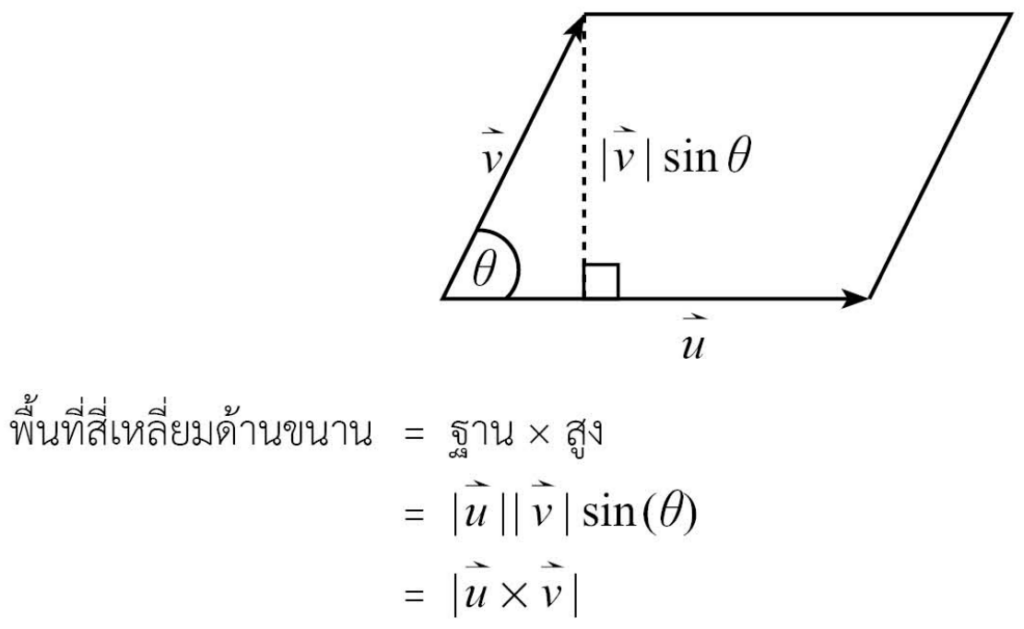
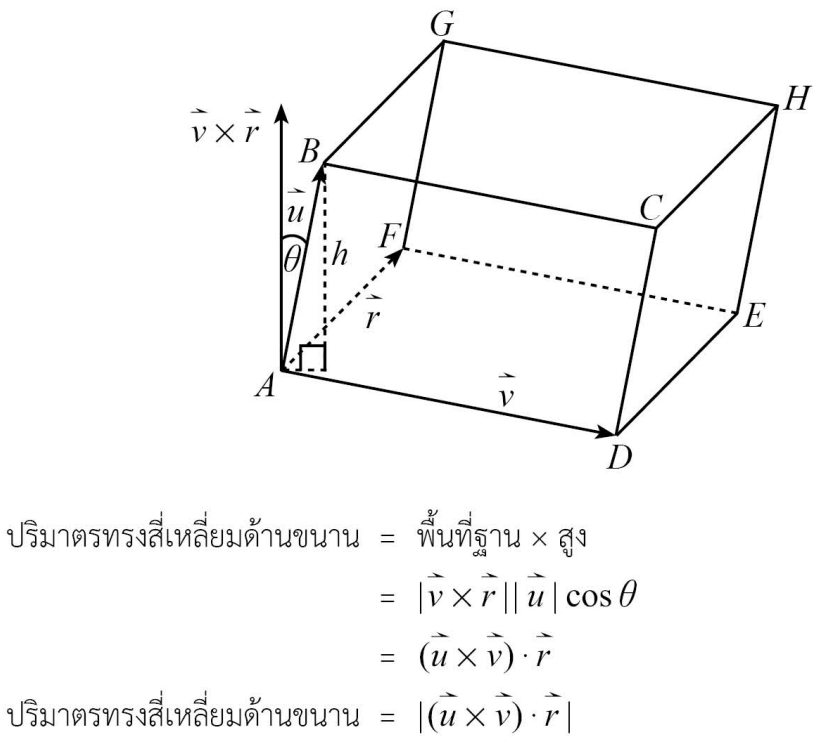
การใช้เวกเตอร์ในการหาปริมาตรทรงสี่เหลี่ยมด้านขนาน
กำหนดให้ \vec{u}, \vec{v}, \vec{r} เป็นเวกเตอร์ใด ๆ เราจะได้ว่า
✨ตัวอย่างที่ 5 จงหาพื้นที่ของรูปสี่เหลี่ยมด้านขนานที่มี \vec{u} = -\vec{i} + 2\vec{j} + \vec{k}, \vec{v} = 3\vec{i} + 4\vec{k} เป็นด้านของรูปสี่เหลี่ยมนี้
วิธีทำ
ในขั้นตอนการหาพื้นที่นั้น เราจะต้องใช้ผลคูณเชิงเวกเตอร์ด้วย ซึ่งก็คือ \vec{u} \times \vec{v} ซึ่งเราได้ทำการหาไว้แล้วในตัวอย่างที่ 4 ครับ ดังนั้น เราจะหาพื้นที่ของรูปสี่เหลี่ยมด้านขนานนี้ได้ดังนี้
|\vec{u} \times \vec{v}| = |8\vec{i} + 7\vec{j} – 6\vec{k}| = \sqrt{8^2 + 7^2 + 6^2} = \sqrt{64+ 49 + 36} = \sqrt{149} ตารางหน่วย
ดังนั้นพื้นที่ของรูปสี่เหลี่ยมด้านขนานรูปนี้เท่ากับ \sqrt{149} ตารางหน่วย
เป็นยังไงกันบ้างครับ สำหรับเนื้อหาเวกเตอร์ที่พี่นำมาฝากน้อง ๆ ทุกคนในวันนี้ หลายคนอาจจะยังไม่เข้าใจในครั้งแรกที่อ่าน แต่เราไม่จำเป็นต้องเข้าใจเนื้อหาทั้งหมดนี้ภายในวันเดียวหรือการอ่านเพียงรอบเดียวก็ได้ครับ น้อง ๆ สามารถค่อย ๆ ทบทวนเนื้อหาไปพร้อมกับการฝึกทำโจทย์เพื่อให้เก่งขึ้นได้
ถ้าน้องๆ คิดว่าแค่อ่านบทความแล้วยังไม่พอ พี่ออนดีมานด์มีคอร์สเรียนแนะนำดีๆ มาบอกต่อ
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์