✨เนื้อหา อสมการเชิงเส้นตัวแปรเดียว ม.3
เมื่อพูดถึงสมการ น้อง ๆ หลายคนอาจจะนึกออกทันที เพราะเป็นบทเรียนสำคัญที่เราเคยเจอกันมาแล้วในวิชาคณิตศาสตร์ แต่หากพูดถึงอีกเรื่องหนึ่งที่สำคัญไม่แพ้สมการเลยก็คือ อสมการเชิงเส้นตัวแปรเดียว นั่นเองครับ เพราะเราสามารถใช้อสมการในการวิเคราะห์เชิงเปรียบเทียบ อีกทั้งยังสามารถช่วยแก้ปัญหาของโจทย์ต่าง ๆ ได้อีกด้วย วันนี้พี่จะมาอธิบายให้เข้าใจว่าอสมการเชิงเส้นตัวแปรเดียวคืออะไร พร้อมทั้งมีสรุปเนื้อหาและแบบฝึกหัดให้ลองทำด้วย ถ้าทุกคนพร้อมแล้ว ไปเริ่มกันเลย!
✨อสมการคืออะไร?
อสมการ (Inequality) คือ ความสัมพันธ์ระหว่างปริมาณสองค่าที่ไม่เท่ากัน คำว่า “อสมการ” มาจากคำว่า “สมการ” ที่แปลว่าเท่ากัน แต่ในอสมการ ตัวแปรสองฝั่งจะไม่จำเป็นต้องเท่ากัน ตัวอย่างเช่น x+2 > 5 หมายความว่า ค่า x+2 นั้นมากกว่า 5 ซึ่งไม่ใช่การเท่ากันเหมือนสมการครับ
เครื่องหมายที่ใช้ในอสมการ
📌 > มากกว่า
📌 < น้อยกว่า
📌 \geqslant มากกว่าหรือเท่ากับ
📌 \leqslant น้อยกว่าหรือเท่ากับ
เส้นจำนวน
รูปต่อไปนี้คือรูปของเส้นจำนวนที่น้อง ๆ จะได้เห็นบ่อย ๆ หลังจากนี้ครับ
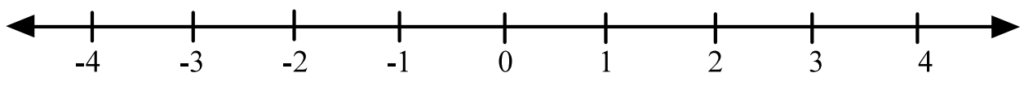
เส้นจำนวนจะช่วยให้เรามองภาพคำตอบของอสมการแต่ละข้อได้ง่ายขึ้น
✨อสมการแตกต่างจากสมการยังไง?
สมการ เป็นการหาค่าที่ทำให้ทั้งสองฝั่งของเครื่องหมายเท่ากันเสมอ เช่น 3x+2 = 11 เราจะแก้หาค่า x ที่ทำให้ทั้งสองฝั่งของสมการมีค่าเท่ากัน ในที่นี้ค่า x จะเป็นตัวเลขเดียวที่ทำให้สมการเป็นจริงครับ
อสมการ แตกต่างกันตรงที่ว่ามันไม่จำเป็นต้องหาเพียงค่าหนึ่งเดียวของตัวแปร แต่สามารถมีค่าได้หลายค่าที่ทำให้เงื่อนไขเป็นจริง เช่น x+3 > 7 เราจะทราบได้ทันทีว่าค่าของ x สามารถเป็นได้ทั้ง 5, 6, 7 หรือมากกว่านี้ก็ได้ เพราะทุกค่าที่มากกว่า 4 จะทำให้อสมการนี้เป็นจริง นั่นแปลว่าคำตอบของอสมการจะไม่ใช่แค่ตัวเลขตัวเดียว แต่เป็นกลุ่มของตัวเลขที่สอดคล้องกับเงื่อนไขของอสมการนั่นเองครับ
✨อสมการเชิงเส้นตัวแปรเดียวคืออะไร?
อสมการเชิงเส้นตัวแปรเดียว หมายถึง อสมการที่มีเพียงตัวแปรหนึ่งตัว เช่น x และจะมีเลขชี้กำลังเป็น 1 เท่านั้น โดยตำแหน่งที่ปรากฎตัวแปรนั้นสามารถมีได้หลายจุดก็ได้ แต่ขอแค่ให้ตัวแปรเหล่านั้นเป็นตัวแปรตัวเดียวกันครับ พี่ขอยกตัวอย่างอสมการเชิงเส้นตัวแปรเดียวให้น้อง ๆ ดูสัก 2 อสมการนะครับ
📌 2x+3 > 7
📌 3x+5 \leqslant x-2
✨คำตอบของอสมการเชิงเส้นตัวแปรเดียว
เมื่อเราพิจารณาถึงลักษณะคำตอบของอสมการเชิงเส้นตัวแปรเดียว เราจะสามารถแบ่งลักษณะคำตอบออกมาได้เป็น 3 ลักษณะดังนี้ครับ
📌 มีจำนวนจริงบางจำนวนเป็นคำตอบ
เช่น x+3 > 1
📌 มีจำนวนจริงทุกจำนวนเป็นคำตอบ
เช่น x-1 < x
📌 ไม่มีจำนวนจริงใดเป็นคำตอบ
เช่น x+1 \geqslant x+5
✨เส้นจำนวนแสดงคำตอบของอสมการ
โดยทั่วไปแล้วการแสดงผลคำตอบอสมการเชิงเส้นตัวแปรเดียวนั้นเรามักจะเขียนเส้นจำนวน ประกอบด้วย เพราะเส้นจำนวนจะช่วยให้เราเห็นช่วงคำตอบของอสมการนั้น ๆ ได้ชัดเจนขึ้นมากยิ่งขึ้นนั่นเองครับ ต่อไปนี้จะเป็นสัญลักษณ์ที่น้อง ๆ ควรรู้เกี่ยวกับการเขียนเส้นจำนวนครับ

เพื่อให้เห็นภาพมากขึ้น พี่ขอยกตัวอย่างเป็นเส้นจำนวนที่แสดงคำตอบของอสมการ -2 < x \leqslant 4 ดังรูปต่อไปนี้ครับ

การแก้อสมการเชิงเส้นตัวแปรเดียว
สมบัติต่าง ๆ ต่อไปนี้เราจะเรียกว่า สมบัติของการไม่เท่ากัน (Properties of inequality) ครับ โดยจะกำหนดให้ a, b และ c เป็นจำนวนจริง
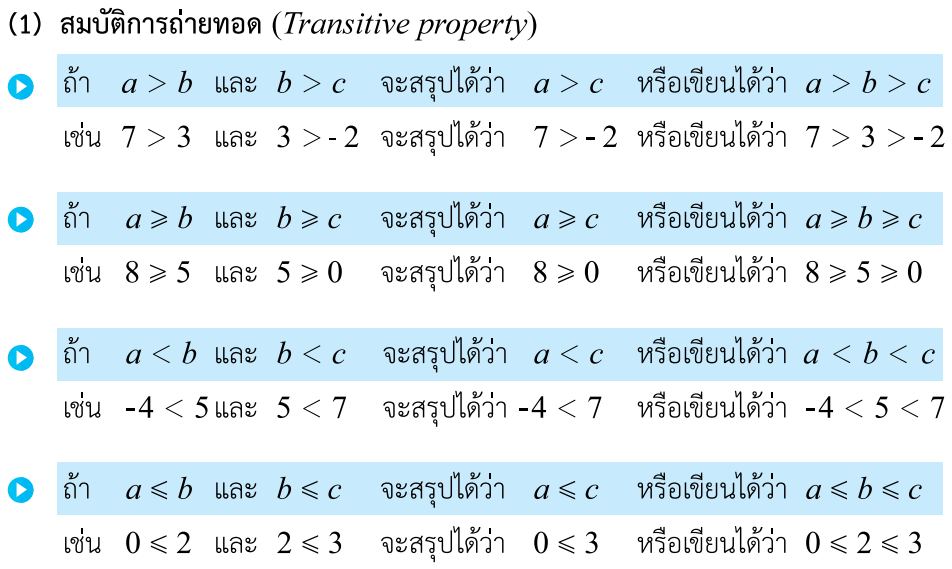




เมื่อเราได้เรียนรู้เกี่ยวกับสมบัติของความไม่เท่ากันแล้ว ต่อไปเราจะนำสมบัติเหล่านี้ไปใช้ในการแก้อสมการ
ตัวอย่างที่ 1 จงแก้อสมการ 6-3x > -18
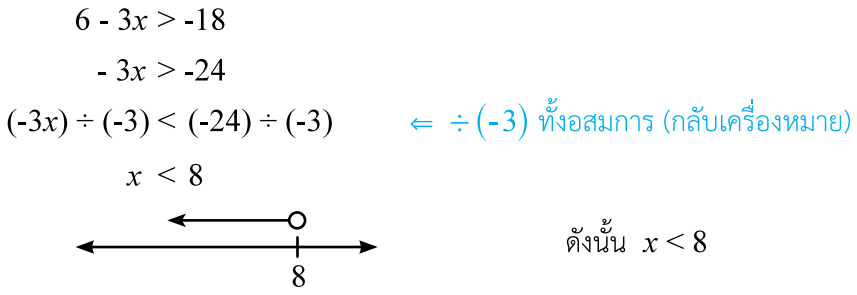
เมื่อเราได้ลองแก้อสมการจากตัวอย่างไปแล้ว ต่อไปพี่จะพาน้อง ๆ ไปรู้จักกับการแก้ปัญหาของโจทย์ปัญหาในชีวิตประจำวันที่สามารถใช้อสมการเชิงเส้นตัวแปรเดียวมาแก้ไขได้กันครับ
โจทย์ปัญหาเกี่ยวกับการแก้อสมการเชิงเส้นตัวแปรเดียว
✨ขั้นตอนการแก้โจทย์ปัญหาอสมการเชิงเส้นตัวแปรเดียว
- อ่านและทำความเข้าใจโจทย์
- กำหนดตัวแปรในสิ่งที่โจทย์ถาม
- สร้างอสมการจากข้อมูลที่โจทย์ให้มา
- แก้อสมการ
- ตรวจคำตอบ
เมื่อเราได้รู้ถึงขั้นตอนวิธีการแก้โจยท์ปัญหาเกี่ยวกับอสมการเชิงเส้นตัวแปรเดียวแล้ว ต่อไปเราจะไปลองทำโจทย์จริง ๆ กัน!
✨ตัวอย่างที่ 2 คุณแม่มีเงิน 500 บาท เธอวางแผนซื้อขนมราคา 20 บาทต่อชิ้น คุณแม่ต้องซื้อขนมอย่างน้อยกี่ชิ้นถึงจะใช้เงินเกิน 300 บาท
วิธีทำ
- อ่านและทำความเข้าใจโจทย์
คุณแม่ต้องการซื้อขนมชิ้นละ 20 บาท อยากรู้ว่าซื้อกี่ชิ้นจะใช้เงินเกิน 300 บา - กำหนดตัวแปรในสิ่งที่โจทย์ถาม
กำหนดให้ x คือจำนวนขนมที่คุณแม่ต้องซื้อ - สร้างอสมการจากข้อมูลที่โจทย์ให้มา
จากโจทย์จะได้อสมการคือ 20x > 300 - แก้อสมการ
จากอสมการคือ 20x > 300
เราทำการหารด้วย 20 ทั้งสองข้างของอสมการ จะได้
x > \dfrac{300}{20}
x > 15 - ตรวจคำตอบ
จากขั้นตอนที่ 4. เราทราบว่าุคณแม่ต้องซื้อขนมมากกว่า 15 ชิ้น จึงจะใช้เงินเกิน 300 บาท
นั่นหมายความว่าคุณแม่ต้องซื้อขนมอย่างน้อย 16 ชิ้น
ตรวจสอบคำตอบโดยการนำ 16 คูณกับ 20 เพื่อหาจำนวนเงินทั้งหมดที่คุณแม่ต้องใช้ จะได้ 16 \times 20 = 320 พบว่าเกิน 300 บาทตามที่โจทย์ต้องการ
ตอบ คุณแม่ต้องซื้อขนมอย่างน้อย 16 ชิ้น
✨ตัวอย่างที่ 3 พอลต้องการซื้อตั๋วภาพยนตร์ที่ราคา 120 บาทต่อตั๋ว พอลมีเงินอยู่ 600 บาท อยากทราบว่าพอลสามารถซื้อตั๋วหนังได้มากที่สุดกี่ใบ
วิธีทำ
- อ่านและทำความเข้าใจโจทย์
ตั๋วภาพยนตร์ใบละ 120 บาท และพอลมีเงิน 600 บาท อยากทราบว่าพอลจะซื้อตั๋วหนังได้กี่ใบ - กำหนดตัวแปรในสิ่งที่โจทย์ถาม
กำหนดให้ x คือจำนวนตั๋วที่พอลซื้อได้ - สร้างอสมการจากข้อมูลที่โจทย์ให้มา
จากโจทย์จะได้อสมการคือ 120x \leqslant 600 - แก้อสมการ
จากอสมการ 120x \leqslant 600
ทำการหารด้วย 120 ทั้งสองข้างของอสมการ จะได้
x \leqslant \dfrac{600}{120}
นั่นคือ x \leqslant 5 - ตรวจคำตอบ
จากขั้นตอนที่ 4. เราทราบว่าพอลสามารถซื้อตั๋วหนังได้มากที่สุด 5 ใบ ตรวจสอบโดยการนำ 5 ไปคูณกับ 120 จะได้ 5 \times 120 = 600 ซึ่งยังไม่เกินจำนวนเงินที่พอลมี ดังนั้นคำตอบจึงถูกต้อง
ตอบ พอลสามารถซื้อตั๋วหนังได้มากที่สุด 5 ใบ
✨ตัวอย่างที่ 4 สามเท่าของจำนวนเต็มบวกจำนวนหนึ่งมากกว่า 15 อยู่ไม่เกิน 9 จำนวนเต็มบวกที่เป็นไปได้มีจำนวนใดบ้าง
วิธีทำ
- อ่านและทำความเข้าใจโจทย์โจทย์ต้องการหาจำนวนเต็มบวกทั้งหมดที่เป็นไปได้ ที่สอดคล้องกับเงื่อนไขดังกล่าว
- กำหนดตัวแปรในสิ่งที่โจทย์ถามกำหนดให้ x คือจำนวนเต็มบวกนั้น
- สร้างอสมการจากข้อมูลที่โจทย์ให้มา
จากโจทย์ เราจะได้อสมการคือ 15 < 3x \leqslant 24 - แก้อสมการ
จากอสมการ 15 < 3x \leqslant 24
ทำการหารด้วย 3 ทั้งอสมการ
จะได้ \dfrac{15}{3} < x \leqslant \dfrac{24}{3}
หรือก็คือ 5 < x \leqslant 8 - ตรวจคำตอบ
จากการแก้อสมการ ทำให้เราทราบว่าจำนวนเต็มบวกที่เป็นไปได้ทั้งหมดคือ 6, 7 หรือ 8 เราสามารถตรวจคำตอบโดยการนำจำนวนเหล่านี้ไปคูณกับ 3 จะได้ 3(6) = 16, 3(7) = 21, 3(8) = 24 ซึ่งผลลัพธ์ที่ได้นั้น มากกว่า 15 และมากกว่าอยู่ไม่เกิน 9 จริง ดังนั้นคำตอบจึงถูกต้อง
ตอบ จำนวนเต็มบวกที่เป็นไปได้คือ 6, 7 และ 8
✨ตัวอย่างที่ 5 กันต์อ่านหนังสือวันแรกได้ \dfrac{2}{5} ของเล่ม วันต่อมาอ่านได้ 31 หน้า รวมสองวันอ่านได้มากกว่าครึ่งเล่ม อยากทราบว่าหนังสือเล่มนี้มีจำนวนหน้าอย่างมากกี่หน้า
วิธีทำ
- อ่านและทำความเข้าใจโจทย์
วันแรกอ่านได้ \dfrac{2}{5} ของเล่ม
วันต่อมาอ่านได้ 31 หน้า
รวมสองวัน อ่านได้เกินครึ่งเล่ม
อยากทราบว่าหนังสือเล่มนี้มีจำนวนหน้าอย่างมากกี่หน้า - กำหนดตัวแปรในสิ่งที่โจทย์ถามกำหนดให้จำนวนหน้าทั้งหมดของหนังสือเล่มนี้คือ x
- สร้างอสมการจากข้อมูลที่โจทย์ให้มา
จากโจทย์ เราจะได้อสมการคือ \dfrac{2}{5}x + 31 > \dfrac{1}{2}x - แก้อสมการ
ลบด้วย \dfrac{1}{2}x ทั้งสองข้างของอสมการ
จะได้ \dfrac{2}{5}x – \dfrac{1}{2}x + 31 > 0
รวมพจน์ตัวแปร จะได้ \dfrac{4}{10}x-\dfrac{5}{10}x + 31 > 0
หรือก็คือ -\dfrac{1}{10}x + 31 > 0
ทำการบวกด้วย \dfrac{1}{10}x ทั้งสองข้างของอสมการ
จะได้ 31 > \dfrac{1}{10}x
คูณด้วย 10 ทั้งสองข้างของอสมการ
จะได้ 310 > x - ตรวจคำตอบ
จากการแก้อสมการ ทำให้เราทราบว่า x ซึ่งคือจำนวนหน้าหนังสือ ต้องน้อยกว่า 310 ดังนั้นจำนวนหน้าหนังสือที่เป็นไปได้มากที่สุดที่ควรจะเป็นคือ 309 หน้า ดังนั้นเราจึงนำ 309 ไปลองแทนในอสมการที่เราได้ตั้งไว้
จะได้ \dfrac{2}{5}(309) + 31 > \dfrac{1}{2}(309)
หรือก็คือ 123.6 + 31 > 154.5
นั่นคือ 154.6 > 154.5
ซึ่งอสมการเป็นจริง
ตอบ หนังสือเล่มนี้มีจำนวนหน้าอย่างมาก 309 หน้า
✨ตัวอย่างที่ 6 ร้านขายขนมปังแห่งหนึ่งมีต้นทุนในการผลิตขนมปัง x ชิ้นต่อวันคือ 960 + 3x บาท ถ้าร้านขายขนมปังชนิดนี้ชิ้นละ 15 บาท อยากทราบว่าร้านขนมปังต้องผลิตขนมปังอย่างต่ำวันละกี่ชิ้นจึงจะได้กำไร
วิธีทำ
- อ่านและทำความเข้าใจโจทย์
ร้านขายขนมปังแห่งหนึ่งมีต้นทุนในการผลิตขนมปัง x ชิ้นต่อวันคือ 960 + 3x บาท
ขายไปชิ้นละ 15 บาท
อยากทราบว่าร้านขนมปังต้องผลิตขนมปังอย่างต่ำวันละกี่ชิ้นจึงจะได้กำไร - กำหนดตัวแปรในสิ่งที่โจทย์ถามเนื่องจากโจทย์กำหนดตัวแปรมาให้แล้ว เราจึงไม่จำเป็นต้องกำหนดตัวแปรเพิ่มเติมครับ นั่นคือโจทย์กำหนดให้ว่าจำนวนขนมปังที่ที่ผลิตต่อวันคือ x ชิ้น
- สร้างอสมการจากข้อมูลที่โจทย์ให้มา
จากโจทย์ เราจะได้อสมการคือ 15x – (960 + 3x) > 0 - แก้อสมการ
ทำการเปิดวงเล็บ 15x – 960 – 3x > 0
จากนั้นรวมพจน์ที่เป็นตัวแปร 12x – 960> 0
บวกด้วย 960 ทั้งสองข้างของอสมการ
จะได้ 12x > 960
หารด้วย 12 ทั้งสองข้างของอสมการ
จะได้ x > \dfrac{960}{12}
หรือก็คือ x > 80 - ตรวจคำตอบ
จากการแก้อสมการ ทำให้เราพบว่าจำนวนขนมปังที่ผลิตในแต่ละวัน ต้องมากกว่า 80 จึงจะได้กำไร ดังนั้นจำนวนขนมปังที่ร้านต้องผลิตอย่างต่ำในแต่ละวันต้องเป็น 81 ชิ้น เราจึงนำ 81 ไปลองแทนในอสมการที่เราตั้งไว้
จะได้ 15(81) – (960 + 3(81)) > 0
1215 – (960 + 243) > 0
1215 – 1203 > 0
12 > 0
ซึ่งอสมการเป็นจริง
ตอบ ร้านขนมปังต้องผลิตขนมปังอย่างต่ำวันละ 81 ชิ้น จึงจะได้กำไร
เป็นยังไงกันบ้างครับ สำหรับเนื้อหาอสมการเชิงเส้นตัวแปรเดียวที่พี่นำมาฝากน้อง ๆ ทุกคนในวันนี้ น้อง ๆ หลายคนอาจจะอ่านแล้วยังไม่เข้าใจในทันที แต่เราไม่จำเป็นต้องเข้าใจเนื้อหาทั้งหมดนี้ภายในวันเดียวหรือการอ่านเพียงรอบเดียวก็ได้ครับ เราสามารถค่อย ๆ ทบทวนเนื้อหาไปพร้อมกับการฝึกทำโจทย์เพื่อให้เก่งขึ้นได้ ถ้ารู้กสึกว่าแค่อ่านบทความแล้วไม่พอ พี่ออนดีมานด์ มีคอร์สเรียนแนะนำสำหรับน้อง ม.3 มาบอก

บทความอื่นๆ เพิ่มเติม 👉 : OnDemand