สวัสดีน้อง ๆ ทุกคนครับ! วันนี้เราจะมาพูดถึงเรื่องที่ฟังแล้วอาจทำให้หลายคนคิดถึงอดีตตอน ม.3 นั่นก็คือ “ตรีโกณมิติ” แต่คราวนี้จะไม่ใช่แค่การทบทวนสิ่งที่น้อง ๆ เคยเรียนไปแล้วเท่านั้น เพราะรอบนี้เราจะลงลึกไปในเรื่อง “ฟังก์ชันตรีโกณมิติ” ที่ซับซ้อนและท้าทายยิ่งขึ้น แต่ไม่ต้องกังวล พี่จะช่วยให้เรื่องนี้กลายเป็นเรื่องง่าย ๆ ด้วยการอธิบายแบบเข้าใจง่าย มีตัวอย่างเจ๋ง ๆ พร้อมสูตรเด็ดที่ควรรู้ ถ้าน้อง ๆ ทุกคนพร้อมแล้ว ไปลุยกันเลย!
✨ความแตกต่างระหว่างตรีโกณมิติ ม.3 และ ม.5
น้อง ๆ คงสงสัยกันใช่ไหมครับว่าเราเคยเรียนตรีโกณมิติกันไปแล้วในช่วงประมาณตอน ม.3 แล้วทำไมพอขึ้น ม.5 มาแล้วยังต้องมาเรียนเรื่องนี้ซ้ำอีกรอบ แล้วมันต่างกันกับตอน ม.3 ยังไง ในหัวข้อนี้เราจะมาทำความเข้าใจถึงข้อแตกต่างนั้นกันครับ
ตอน ม.3 ตอนนั้นตรีโกณมิติคือเรื่องของการคำนวณความสัมพันธ์ระหว่างด้านของสามเหลี่ยมมุมฉากกับมุม เราได้รู้จักกับสามฟังก์ชันหลักคือ ไซน์ (Sine), โคไซน์ (Cosine) และ แทนเจนต์ (Tangent) ตอนนั้นเราแค่เน้นหาค่าความสัมพันธ์ระหว่างมุมกับด้านในสามเหลี่ยมมุมฉากเพียงเท่านั้นครับ แต่มาถึง ม.5 ตรีโกณมิติไม่ได้อยู่แค่ในสามเหลี่ยมอีกต่อไป! เราจะเรียนรู้ฟังก์ชันตรีโกณมิติในเชิงลึกมากขึ้น ซึ่งสามารถนำไปใช้ได้หลากหลายทั้งในการวิเคราะห์การเคลื่อนที่ การแก้สมการ และการเขียนกราฟ เราจะได้รู้จักกับฟังก์ชันผกผัน การวัดมุมเป็นหน่วยเรเดียน และแนวคิดต่าง ๆ ที่ช่วยให้เราประยุกต์ตรีโกณมิติไปใช้ในชีวิตประจำวันได้มากขึ้นนั่นเองครับ
✨ความหมายของฟังก์ชันตรีโกณมิติ
ฟังก์ชันตรีโกณมิติคือฟังก์ชันที่แสดงความสัมพันธ์ระหว่างมุมกับอัตราส่วนของด้านในสามเหลี่ยมมุมฉาก

เมื่อเราพิจารณาที่มุม A เราจะได้ว่า
\sin A = \dfrac{\text{ ความยาวด้านตรงข้ามมุม } A}{\text{ ความยาวด้านตรงข้ามมุมฉาก}} = \dfrac{BC}{AB}
\cos A = \dfrac{\text{ ความยาวด้านประชิดมุม } A}{\text{ ความยาวด้านตรงข้ามมุมฉาก}} = \dfrac{AC}{AB}
\tan A = \dfrac{\text{ ความยาวด้านตรงข้ามมุม } A}{\text{ ความยาวด้านประชิดมุม } A} = \dfrac{BC}{AC}
\csc A = \dfrac{1}{\sin A} = \dfrac{AB}{BC}
\sec A = \dfrac{1}{\cos A} = \dfrac{AB}{AC}
\cot A = \dfrac{1}{\tan A} = \dfrac{AC}{BC}
✨การวัดมุม
หน่วยในการวัดมุมที่มักใช้กันบ่อย ๆ ในตรีโกณมิติจะมีอยู่ด้วยกัน 2 หน่วย คือ องศา (degree) และเรเดียน (radian) โดยหน่วยองศานั้น น้อง ๆ อาจจะคุ้นเคยกันดีอยู่แล้ว แต่หน่วยเรเดียนอาจจะยังเป็นหน่วยในการวัดมุมที่ใหม่สำหรับน้อง ๆ หลายคน ดังนั้นพี่ขออธิบายเพิ่มเติมเรื่องหน่วยเรเดียนดังนี้ครับ
หากเราพิจารณาวงกลมวงหนึ่งที่มีรัศมี r เราจะพบว่ามุมที่จุดศูนย์กลางของวงกลม \theta ที่รองรับด้วยส่วนโค้งที่มีความยาว s เราจะมีความสัมพันธ์คือ \theta = \dfrac{s}{r} โดยมีหน่วยเป็นเรเดียน
เนื่องจากมุมที่จุดศูนย์กลางของวงกลมใด ๆ จะมีขนาด 2\pi เรเดียน เสมอ ดังนั้นเราจะได้ความสัมพันธ์ระหว่างมุมในหน่วยองศา และเรเดียน คือ 360^\circ = 2\pi เรเดียน หรือก็คือ 180^\circ = \pi เรเดียน นั่นเองครับ
✨ค่าตรีโกณมิติพื้นฐานที่ควรรู้
เมื่อเราได้รู้ถึงหน่วยในการวัดมุมไปแล้ว ในหัวข้อนี้น้อง ๆ จะได้รู้จักกับค่าตรีโกณมิติของมุมพื้นฐานที่เราควรจะรู้ครับ
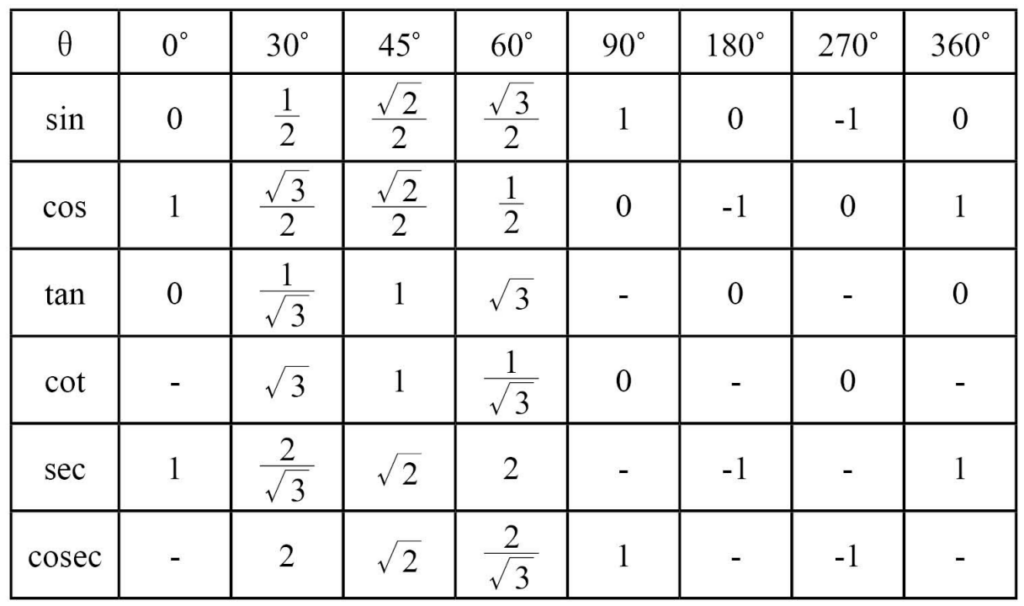
✨สูตรของฟังก์ชันตรีโกณมิติที่ควรรู้
พี่ขอแบ่งสูตรของฟังก์ชันตรีโกณมิติออกเป็นกลุ่ม ๆ ดังนี้ครับ
✨เอกลักษณ์ตรีโกณมิติ
\sin^2 \theta + \cos^2 \theta = 1
1 + \cot^2 \theta = \csc^2 \theta เมื่อ sin \theta \neq 1
\tan^2 \theta + 1 = \sec^2 \theta เมื่อ cos \theta \neq 1
✨สูตรผลบวก ผลต่างมุม
\sin (A+B) = \sin A \cos B + \cos A \sin B
\sin (A-B) = \sin A \cos B – \cos A \sin B
\cos (A+B) = \cos A \cos B – \sin A \sin B
\cos (A-B) = \cos A \cos B + \sin A \sin B
\tan (A+B) = \dfrac{\tan A + \tan B}{1 – \tan A \tan B} เมื่อ \tan A \tan B \neq 1
\tan (A-B) = \dfrac{\tan A – \tan B}{1 + \tan A \tan B} เมื่อ \tan A \tan B \neq -1
✨สูตรผลบวก ผลต่างของตรีโกณ
\sin A + \sin B = 2 \sin \dfrac{A+B}{2} \cos \dfrac{A-B}{2}
\sin A – \sin B = 2 \cos \dfrac{A+B}{2} \sin \dfrac{A-B}{2}
\cos A + \cos B = 2 \cos \dfrac{A+B}{2} \cos \dfrac{A-B}{2}
\cos A – \cos B = -2 \sin \dfrac{A+B}{2} \sin \dfrac{A-B}{2}
✨สูตรมุมสองเท่า
\sin 2 A = 2 \sin A \cos A
\sin 2 A = \dfrac{2\tan A}{1 + \tan^2 A}
\cos 2 A = \cos^2 A – \sin^2 A
\cos 2 A = 2 \cos^2 A – 1
\cos 2 A = 1 – 2 \sin^2 A
\cos 2 A = \dfrac{1 – \tan^2 A}{1 + \tan^2 A}
\tan 2 A = \dfrac{2 \tan A}{1 – \tan^2 A} เมื่อ \tan^2 A \neq 1
ตัวอย่างที่ 1 จงหาค่าของ \cos 75^\circ + \cos 15^\circ
วิธีทำ
จากสูตร \cos A + \cos B = 2 \cos \dfrac{A+B}{2} \cos \dfrac{A-B}{2} เราจะได้ว่า
\begin{aligned}\cos 75^\circ + \cos 15^\circ&= 2 \cos \dfrac{75^\circ+15^\circ}{2} \cos \dfrac{75^\circ-15^\circ}{2} \\&= 2 \cos 45^\circ \cos 30^\circ \\&= 2 \times \dfrac{\sqrt{2}}{2} \times \dfrac{\sqrt{3}}{2} \\&= \dfrac{\sqrt{6}}{2}\end{aligned}
ดังนั้น \cos 75^\circ + \cos 15^\circ = \dfrac{\sqrt{6}}{2}
✨สมการตรีโกณมิติ
ในการแก้สมการตรีโกณมิติเราสามารถทำได้เช่นเดียวกันกับการแก้สมการทั่วไปเลยครับ เพียงแต่ในขั้นตอนการแก้สมการตรีโกณมิตินั้น อาจจะต้องมีการใช้สูตรหรือเอกลักษณ์ของตรีโกณมิติมาช่วยในการจัดรูปด้วยครับ และเมื่อเราแก้สมการเรียบร้อยแล้ว หากโจทย์ข้อนั้นไม่ได้กำหนดเอกภพสัมพัทธ์ เราจะต้องตอบในรูปทั่วไปด้วย ซึ่งทำได้โดยการหาคำตอบในช่วง [0, 2\pi] ก่อน แล้วบวกคำตอบนั้น ๆ ด้วย 2n\pi นั่นเองครับ เมื่อทราบแบบนี้แล้ว เรามาลองแก้สมการตรีโกณมิติกันนน
ตัวอย่างที่ 2 กำหนดให้ 0^\circ \leqslant x \leqslant 360^\circ จงหาเซตคำตอบของสมการ 2\sin x \tan x – 2\sin x = 0
วิธีทำ
\begin{aligned}2\sin(x)\tan(x) – 2\sin(x) &= 0 \\2\sin(x)(\tan(x) – 1) &= 0 \\\sin(x) &= 0 \quad \text{ หรือ } \quad \tan(x) – 1 = 0 \\x &= 0^\circ, 360^\circ \quad\text{ หรือ } \quad x = 45^\circ, 225^\circ\end{aligned}
ดังนั้นเซตคำตอบของสมการคือ 0^circ, 45^\circ, 225^\circ, 360^\circ
✨กราฟของฟังก์ชันตรีโกณมิติ
ฟังก์ชันตรีโกณมิติเป็นฟังก์ชันคาบ โดยคาบคือช่วงของ x ที่ทำให้กราฟมีลักษณะเดิม และมีแอมพลิจูดเท่ากับ \dfrac{\operatorname{max} – \operatorname{min}}{2}
กำหนดให้ a และ b เป็นจำนวนจริง และเราพิจารณาสมการ
y = a\sin (bx – h) + k และ
y = a\cos (bx – h) + k
จะมีคาบเท่ากับ \dfrac{2\pi}{b}, แอมพลิจูดเท่ากับ |a|, \operatorname{max} เท่ากับ |a| + k และ \operatorname{min} เท่ากับ -|a| + k และต่อไปนี้คือกราฟของฟังก์ชัน \sin x, \cos x, \tan x ที่น้อง ๆ ควรทราบครับผม
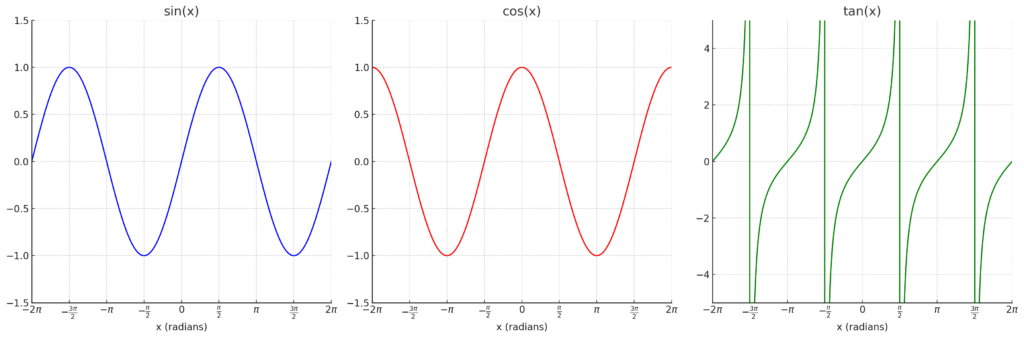
✨ตัวผกผันของฟังก์ชันตรีโกณมิติ
ตัวผกผันของฟังก์ชัน \sin, \cos, \tan จะเป็น \arcsin, \arccos, \arctan ตามลำดับ โดยมีแนวคิดคือ เช่น ถ้าน้องต้องการหาค่าของ \arcsin x มันจะเหมือนกับการที่เราไปพยายามหามุม \theta อะไรซักอย่างนึง ที่ทำให้ \sin \theta = x นั่นเองครับ โดยฟังก์ชัน \arcsin, \arccos, \arctan นั้น จะมีโดเมน และเรนจ์ดังตารางต่อไปนี้ครับ

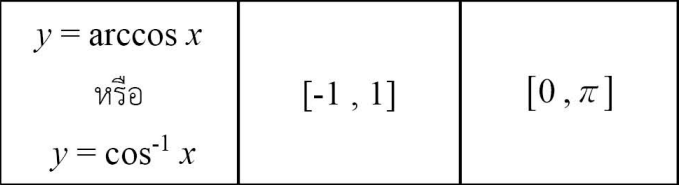

ตัวอย่างที่ 3 จงหาค่าของ \arcsin \dfrac{1}{2} + \arccos 1
วิธีทำ
กำหนดให้ A = \arcsin \dfrac{1}{2}, B = \arccos 1
สิ่งที่เราต้องทำคือ พิจารณาว่า \sin A = \dfrac{1}{2} แล้วมุม A คือมุมอะไร ซึ่งมุมนั้นคือ \dfrac{\pi}{6} นั่นเองครับ เช่นเดียวกันกับ B เราจะพบว่ามุมนั้นคือ 0
ดังนั้นสุดท้ายแล้ว เราจึงได้ว่า \arcsin \dfrac{1}{2} + \arccos 1 = \dfrac{\pi}{6} + 0 = \dfrac{\pi}{6} นั่นเองครับ
กฎของไซน์ กฎของโคไซน์
พิจาณาสามเหลี่ยม ABC กำหนดให้ด้านตรงข้ามมุม A, B และ C มีความยาว a, b และ c ตามลำดับ
กฎของไซน์
มีความสัมพันธ์ดังสมการ \dfrac{\sin A}{a} = \dfrac{\sin B}{b} = \dfrac{\sin C}{c} และเราจะใช้กฎของไซน์เมื่อเรารู้หนึ่งมุมกับด้านตรงข้าม
✨กฎของโคไซน์
เราสามารถเลือกใช้กฎของโคไซน์ได้ตามสถานการณ์ โดยเลือกใช้จากความสัมพันธ์ต่อไปนี้
a^2 = b^2 + c^2 – 2bc \cos A
b^2 = a^2 + c^2 – 2ac \cos B
c^2 = a^2 + b^2 – 2ab \cos C
และเราจะใช้กฎของโคไซน์เมื่อรู้ด้านทุกด้านของสามเหลี่ยม หรือรู้มุม 1 มุม กับด้านประกอบมุมนั้น
ตัวอย่างที่ 4 กำหนดรูปสามเหลี่ยม ABC มีด้านตรงข้ามมุม A, B และ C ยาว a, b และ c หน่วย ตามลำดับ ถ้า b = 3, c = 5, A = 120^\circ จงหา a
วิธีทำ
จากกฎของโคไซน์ a^2 = b^2 + c^2 – 2bc \cos A เราแทนค่าตัวแปรต่าง ๆ ที่โจทย์กำหนดให้ จะได้ดังนี้
\begin{aligned}a^2 &= b^2 + c^2 – 2bc \cos A \\ a^2 &= 3^2 + 5^2 – 2(3)(5) \cos (120^\circ) \\ a^2 &= 9 + 25 – 30(-\dfrac{1}{2}) \\ a^2 &= 34 + 15 \\ a^2 &= 49 \\ a &= 7\end{aligned}
ดังนั้นเราจึงสรุปได้ว่า a = 7 หน่วย
✨การหาระยะทางและความสูง
เราสามารถใช้ตรีโกณมิติในการคำนวณระยะทางหรือความสูงที่ไม่สามารถวัดตรง ๆ ได้ เช่น หากเราต้องการหาความสูงของต้นไม้ เราอาจใช้ฟังก์ชันไซน์หรือแทนเจนต์ในการหาความสัมพันธ์ระหว่างมุมที่มองจากพื้นถึงยอดต้นไม้กับระยะทางที่เรายืนห่างจากต้นไม้แทนได้นั่นเองครับ โดยในการนำตรีโกณมิติไปใช้ในลักษณะนี้นั้น น้อง ๆ จะต้องรู้จักคำอีกสองคำที่สำคัญมาก ๆ คือ มุมก้ม และ มุมเงย นั่นเองครับ
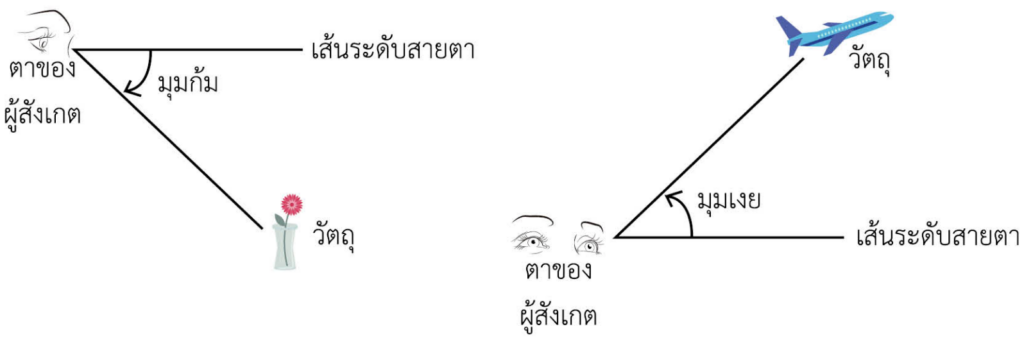
มุมก้ม หมายถึง มุมที่วัดจากเส้นระดับสายตาไปยังเส้นแนวการมองเมื่อวัตถุอยู่ต่ำกว่าเส้นระดับสายตา
มุมเงย หมายถึง มุมที่วัดจากเส้นระดับสายตาไปยังเส้นแนวการมองเมื่อวัตถุอยู่สูงกว่าเส้นระดับสายตา
ตัวอย่างที่ 5 แซมยืนอยู่ห่างจากเสาธง 12 เมตร และแซมวัดมุมเงยจากระดับสายตาของเขาไปถึงยอดเสาธงได้ 45 องศา ถ้าแซมสูง 150 เซนติเมตร แล้วเสาธงสูงเท่าใด
วิธีทำ
จากโจทย์เราจะวาดรูปได้ดังนี้
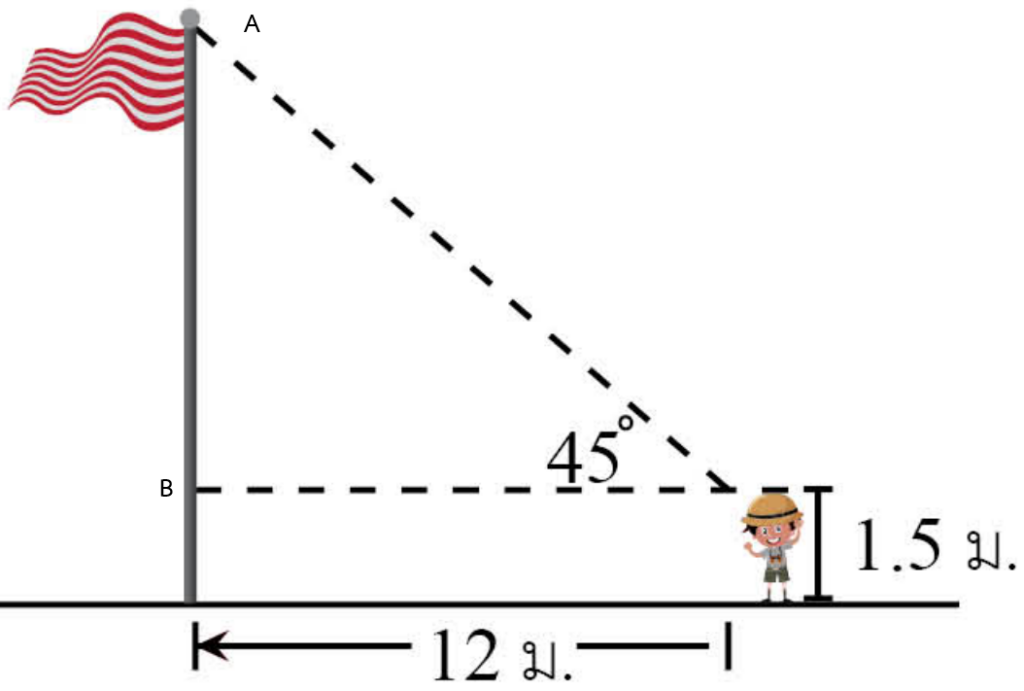
เราจะหาความยาวของ AB ก่อน โดยใช้ \tan 45^\circ เพราะเราทราบว่า \tan 45^\circ = 1 = \dfrac{AB}{12}
นั่นทำให้เราทราบว่า 1 = \dfrac{AB}{12} หรือ AB = 12 เมตร นั่นเอง
ดังนั้นจากรูป เราจะหาความสูงของเสาธงได้จากการนำ AB มารวมกับความสูงของแซม ซึ่งคือ 150 เซนติเมตร
ดังนั้นเสาธงจะมีความสูงเท่ากับ 12 + 1.5 = 13.5 เมตร นั่นเอง
เห็นมั้ยครับว่า ตรีโกณมิติ ม.5 นั้นไม่ใช่เรื่องที่ยากหรือน่ากลัวอย่างที่พวกเราคิด ถ้าเราเข้าใจพื้นฐานตั้งแต่ ม.3 มาแล้ว คราวนี้ก็แค่ต้องลงลึกเข้าไปในรายละเอียดเพิ่มเติมอีกนิดหน่อย เช่น การระบุมุมเป็นเรเดียน การจัดรูป หรือการแก้สมการ การฝึกฝนบ่อย ๆ จะช่วยให้เราเข้าใจตรีโกณมิติมากขึ้นอย่างแน่นอนครับ!
ถ้าน้องไม่เข้าใจตรงไหนสามารถกลับมาดูบทความนี้ได้เสมอเลย หรือถ้าน้องรู้สึกว่า อ่านแค่บทความนี้แล้วไม่พอ พี่ๆ ออนดีมานด์ มีคอร์สเรียนดีๆ สุดคุ้มค่ามาแนะนำๆ
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์

คอร์ส TCAS + ตะลุยโจทย์ คณิต
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand