
สวัสดีน้อง ๆ ทุกคนครับ! วันนี้พี่ ออนดีมานด์จะพาน้อง ๆ ไปรู้จักกับ เรขาคณิตวิเคราะห์และ ภาคตัดกรวย ซึ่งเป็นหัวข้อที่น่าสนใจและมีความสำคัญมากในวิชาคณิตศาสตร์ เรขาคณิตวิเคราะห์เป็นการรวมกันระหว่าง เรขาคณิต และ พีชคณิต โดยเราจะใช้พิกัดและสมการมาอธิบายจุด เส้น และรูปร่างต่าง ๆ บนกราฟได้อย่างละเอียดนั่นเองครับ ถ้าน้อง ๆ พร้อมแล้ว ไปดูเนื้อหากันเลยยย
✨ความแตกต่างของ เรขาคณิต กับ เรขาคณิตวิเคราะห์ และ ภาคตัดกรวย
ในตอน ม.ต้น น้อง ๆ หลายคนอาจจะเคยเรียนเรื่องเรขาคณิต ที่ว่าด้วยการสร้างเส้นตรง หรือการสร้างรูปสามเหลี่ยม สี่เหลี่ยม หรือวงกลม และอาจจะมีการใช้ทฤษฎีบทต่าง ๆ ของวงกลม สามเหลี่ยม หรือสี่เหลี่ยม มาช่วยในการแก้ปัญหาโจทย์แต่ละข้อ เนื้อหาในลักษณะนี้เราจะเรียกว่า “เรขาคณิต” ครับ
สำหรับเรขาคณิตวิเคราะห์และภาคตัดกรวยนั้น จะเป็นการศึกษาโดยเจาะจงไปที่สมการต่าง ๆ ที่นำมาสร้างเป็นรูปเรขาคณิตหรือเส้นตรง และจะให้ความสำคัญไปที่พิกัดของจุดสำคัญ ๆ ต่าง ๆ ของรูปหรือกราฟนั้น ๆ ครับ
โดยจุดที่แตกต่างกันระหว่างสองเรื่องนี้คือ เรขาคณิตนั้นจะไม่ได้สนใจที่สมการของรูปสักเท่าไหร่ แต่จะเน้นที่การนำรูปและทฎษฤีบทต่าง ๆ มาช่วยในการแก้ปัญหา แต่สำหรับเรขาคณิตวิเคราะห์และภาคตัดกรวยนั้น เราจะใช้การวิเคราะห์กราฟ และการแก้สมการในการแก้โจทย์ปัญหาเป็นหลักนั่นเองครับ
✨เรขาคณิตวิเคราะห์
ในหัวข้อนี้เราจะเน้นศึกษาเกี่ยวกับจุดและเส้นตรงเป็นหลัก เราจะไปดูกันว่าถ้ามีจุดกับเส้นตรง เราจะสามารถทำอะไรกับเค้าได้บ้างครับ
ระยะทางระหว่างจุดสองจุด
หากเรามีจุดสองจุดคือ A(x1,y1) และ B(x2,y2) เราจะสามารถหาระยะทางระหว่างสองจุดนั้นได้โดยใช้สูตรต่อไปนี้ครับ
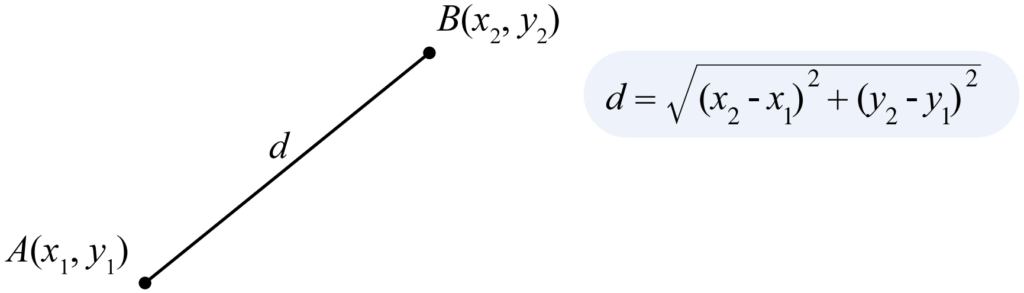
เช่น A(1,2) และ B(3,4) เราจะสามารถหาระยะทาง AB ได้ดังนี้
AB=(3−1)2+(4−2)2=4+4=8=22
หมายความว่า ระยะทางระหว่างจุด A และ B คือ 22 หน่วย นั่นเอง
✨จุดกึ่งกลางของส่วนของเส้นตรง
หากเรามีจุดสองจุดคือ A(x1,y1) และ B(x2,y2) เราจะสามารถหาจุด P ซึ่งเป็นจุดที่อยู่กึ่งกล่างระหว่างสองจุดนี้ได้โดยใช้สูตรต่อไปนี้ครับ
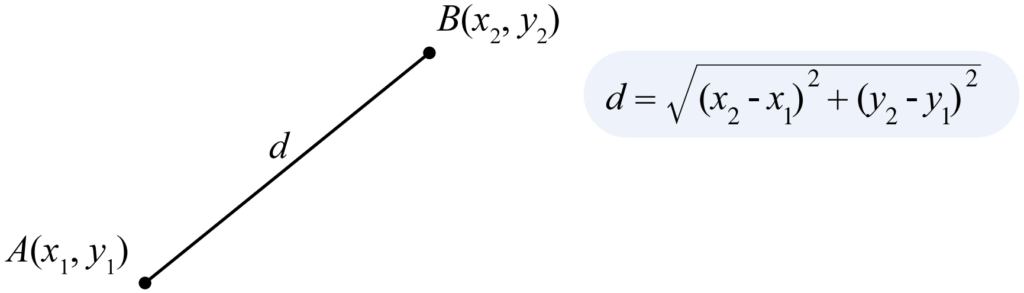
เช่น A(1,2) และ B(3,4) เราจะได้ว่า P(x,y)=P(21+3,22+4)=P(2,3)
✨ระยะทางระหว่าง จุด กับ เส้นตรง
หากเรามีจุดหนึ่งจุดคือ (x1,y1) กับเส้นตรงอีกเส้นหนึ่งคือ Ax+By+C=0 เราจะสามารถหาระยะทางระหว่างจุดกับเส้นตรงดังกล่าวได้โดยใช้สูตรต่อไปนี้ครับ

เช่น จุด (1,2) กับเส้นตรง x+y+1=0 ระยะทางระหว่างจุดและเส้นตรงนี้คือ 12+12∣(1)(1)+(1)(2)+1∣=24=242=22 หน่วย
✨ระยะทางระหว่าง เส้นตรงกับ เส้นตรง
หากเรามีเส้นตรงสองเส้นที่ขนานกันคือ Ax+By+C1=0 และ Ax+By+C2=0 เราสามารถหาระยะทางระหว่างเส้นตรงสองเส้นนี้ได้โดยใช้สูตรต่อไปนี้ครับ
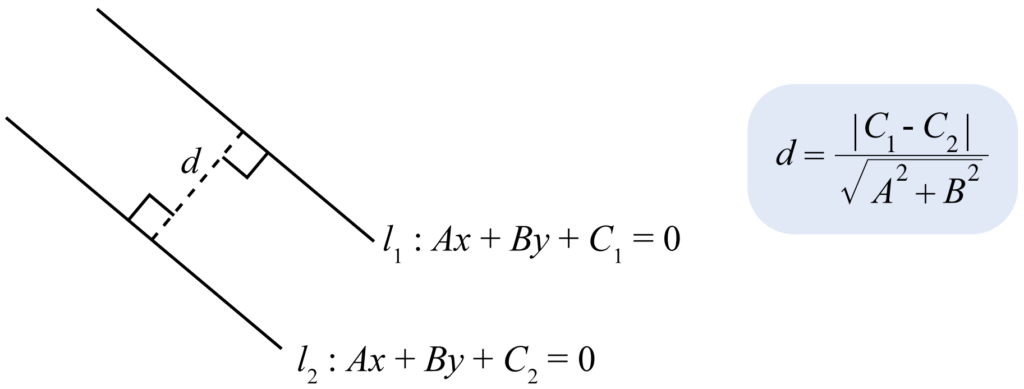
เช่น 3x+4y–7=0 กับ 3x+4y+5=0 มีระยะห่างเท่ากับ 32+42∣−7−5∣=9+16∣−12∣=512=2.4 หน่วย
✨เส้นตรง
เราสามารถเขียนเส้นตรงในรูปของสมการได้ทั้งหมดสองแบบคือ y=mx+c โดยที่ m คือความชันของเส้นตรง และอีกรูปแบบคือ Ax+By+C=0 เมื่อ A,B,C เป็นค่าคงตัวและ A,B ไม่เท่ากับ 0 พร้อมกัน
✨ความชัน
หากเราทราบพิกัดของจุดสองจุด เราจะสามารถหาความชันของเส้งตรงที่เชื่อมจุดสองจุดนั้นได้จากสูตร m=x2–x1y2–y1=x1–x2y1–y2 โดยน้อง ๆ สามารถใช้สูตรไหนก็ได้ครับ เพราะค่าที่ได้จะเท่ากันเสมอ
✨เส้นตรงที่ขนานและตั้งฉากกัน
ถ้าเรามีเส้นตรงสองเส้นคือ l1 ซึ่งมีความชันคือ m1 และ l2 ซึ่งมีความชันคือ m2 เราจะได้ว่า
- ถ้า l1 กับ l2 ขนานกัน จะได้ว่า m1=m2
- ถ้า l1 กับ l2 ตั้งฉากกัน จะได้ว่า m1m2=−1
✨ตัวอย่างที่ 1 เส้นตรงที่ผ่านจุด (2,0),(0,−2) และเส้นตรงที่ผ่านจุด (−1,1),(3,−3) ตั้งฉากกันหรือไม่
✨วิธีทำ
หาความชันของเส้นตรงที่ผ่านจุด (2,0),(0,−2) ได้ดังนี้
0−2−2−0=−2−2=1
หาความชันของเส้นตรงที่ผ่านจุด (−1,1),(3,−3) ได้ดังนี้
3−(−1)−3−1=4−4=−1
หาผลคูณของความชันของเส้นตรงทั้งสอง จะได้ 1×−1=−1
พบว่าผลคูณของความชันมีค่าเท่ากับ −1 เราจึงสรุปได้ว่า ตั้งฉากกัน
✨ภาคตัดกรวย
หากเรามีกรวยอยู่อันหนึ่ง แล้วนำระนาบมาตัดกรวยนั้นในแนวต่าง ๆ กันดังรูป เราจะได้รอยตัดของระนาบกับกรวยนั้น จะเป็นกราฟ 4 ที่เราจะนำมาศึกษาในหัวข้อนี้คือ วงกลม (Circle) วงรี (Ellipse) พาราโบลา (Parabola) และ ไฮเพอร์โบลา (Hyperbola)
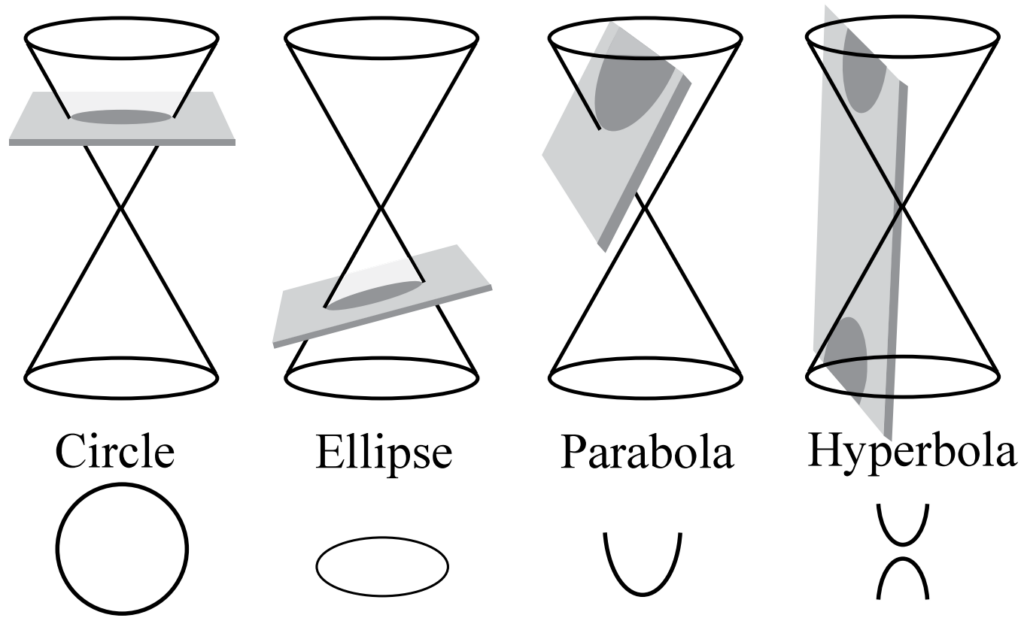
ต่อไปเราจะไปศึกษาภาคตัดกรวยแต่ละตัวกันครับว่ามีรายละเอียดอะไรบ้าง
✨วงกลม
วงกลมโดยนิยามแล้วหมายถึงเซตของจุดทุกจุดบนระนาบซึ่งมีระยะห่างจากจุดคงที่เป็นระยะทางเท่ากัน โดยเราจะเรียกจุดคงที่นั้นว่าจุดศูนย์กลางของวงกลม และเราจะเรียกระยะทางที่เท่ากันนั้นว่ารัศมีของวงกลม
✨ส่วนประกอบของวงกลม
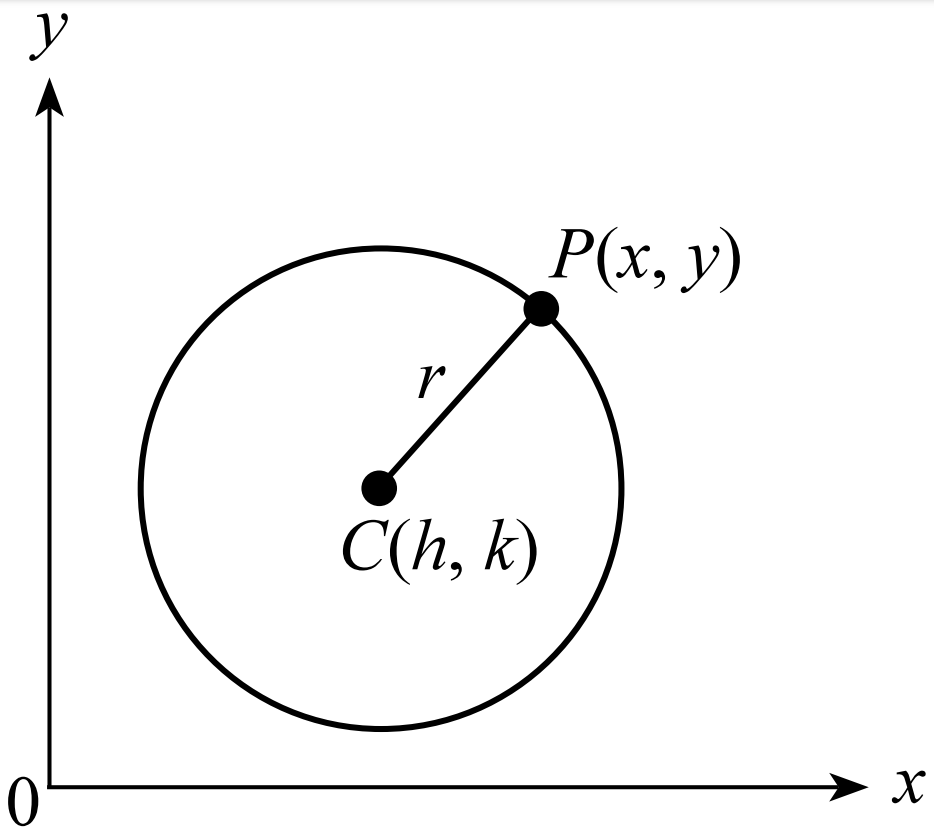
สิ่งที่เราต้องทราบในวงกลมวงหนึ่งคือ จุดศูนย์กลาง C(h,k) และรัศมี r
✨สมการวงกลม
วงกลมมีสมการคือ (x−h)2+(y−k)2=r2
✨ตัวอย่างที่ 2 จงหาจุดศูนย์กลางและรัศมีของวงกลม x2+y2+4x–6y–12=0
✨วิธีทำ
เนื่องจากสมการที่โจทย์กำหนดให้ยังไม่อยู่ในรูปของสมการวงกลมที่เราจะพิจารณา ดังนั้นเราจึงจัดรูปสมการดังนี้ครับ
x2+y2+4x–6y–12(x2+4x)+(y2–6y)(x2+4x+4)+(y2–6y+9)(x+2)2+(y−3)2(x+2)2+(y−3)2=0=12=12+4+9=25=52
จากสมการ เราจึงสรุปได้ว่าจุดศูนย์กลางของวงกลมคือ (−2,3) และรัศมีคือ 5 หน่วย
✨วงรี
วงรีโดยนิยามแล้วหมายถึงเซตของจุดทุกจุดบนระนาบซึ่งมีผลบวกของระยะทางจากจุดใด ๆ ไปยังจุดคงที่สองจุดเป็นค่าคงที่เสมอ โดยเราจะเรียกจุดคงที่ทั้งสองนั้นว่าจุดโฟกัสของวงรี
✨ส่วนประกอบของวงรี
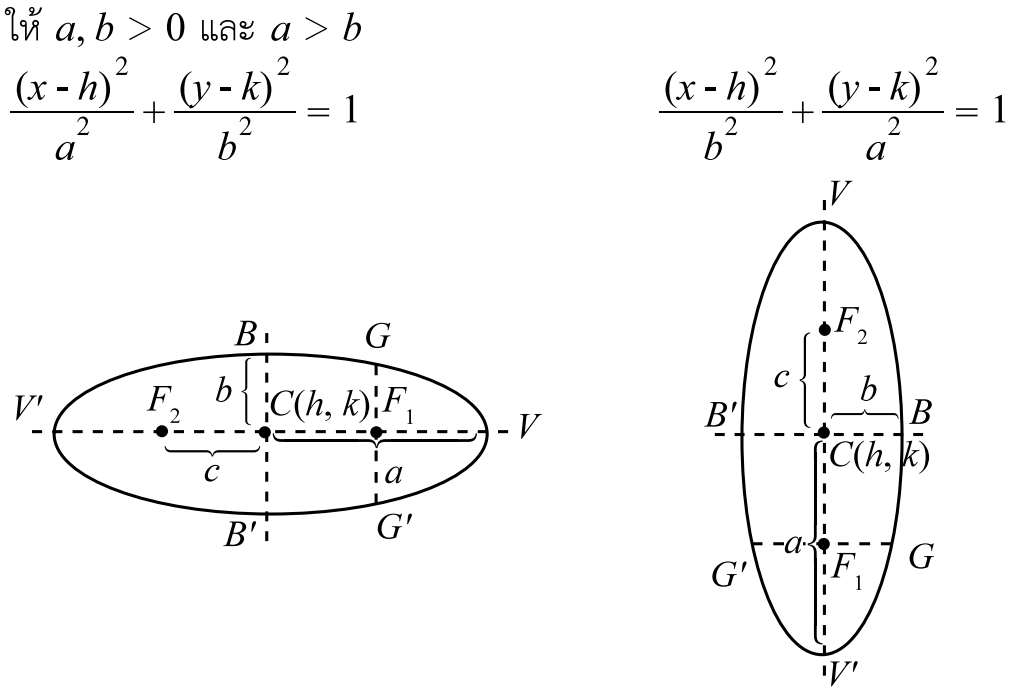
สิ่งที่เราต้องทราบในวงรีคือ จุดศูนย์กลาง C(h,k) แกนเอก คือแกนตามยาวของวงรี มีความยาว 2a และแกนโท คือแกนตามขวางของวงรี มีความยาว 2b
✨สมการวงรี
วงรีที่เราจะสนใจจะมีทั้งหมด 2 แบบครับ คือวงรีนอน และวงรีตั้ง ซึ่งจะมีสมการดังต่อไปนี้ครับ
✨ข้อควรรู้เกี่ยวกับวงรี
- ผลบวกของระยะทางจากจุดใด ๆ บนวงรีไปยังจุดคงที่สองจุดมีค่าคงตัวเสมอ และค่านั้นจะเท่ากับ 2a
- c2=a2−b2 เสมอ
- แกนเอกยาว 2a แกนโทยาว 2b เลตัสเรกตัมยาว a2b2
✨ตัวอย่างที่ 3 กำหนดสมการวงรี 36(x−6)2+16(y+4)2=1 จงหาจุดศูนย์กลางและความยาวแกนเอกของวงรีนี้
✨วิธีทำ
ทำการจัดรูปสมการดังนี้
36(x−6)2+16(y+4)262(x−6)2+42(y+4)2=1=1
จากสมการ เราจึงสรุปได้ว่าจุดศูนย์กลางของวงรีคือ (6,−4) และความยาวแกนเอกคือ 2a=2(6)=12 หน่วย
✨พาราโบลา
พาราโบลาโดยนิยามแล้วหมายถึงเซตของจุดทุกจุดบนระนาบซึ่งอยู่ห่างจากจุดคงที่เป็นระยะทางเท่ากับระยะทางที่จุดนั้นห่างจากเส้นตรงเส้นหนึ่ง โดยเราจะเรียกจุดคงที่นั้นว่าจุดโฟกัสของพาราโบลา และเราจะเรียกเส้นตรงเส้นนั้นว่าเส้นไดเรกตริกซ์
✨ส่วนประกอบของพาราโบลา
สิ่งที่เราต้องทราบในพาราโบลาคือ จุดยอด V(h,k) จุดโฟกัส F เส้นไดเรกตริกซ์ l และระยะโฟกัส c
✨สมการพาราโบลา
พาราโบลาที่เราจะสนใจจะมีทั้งหมด 2 แบบครับ คือพาราโบลาในแนวตั้ง และพาราโบลาในแนวนอน ซึ่งจะมีสมการดังต่อไปนี้ครับ
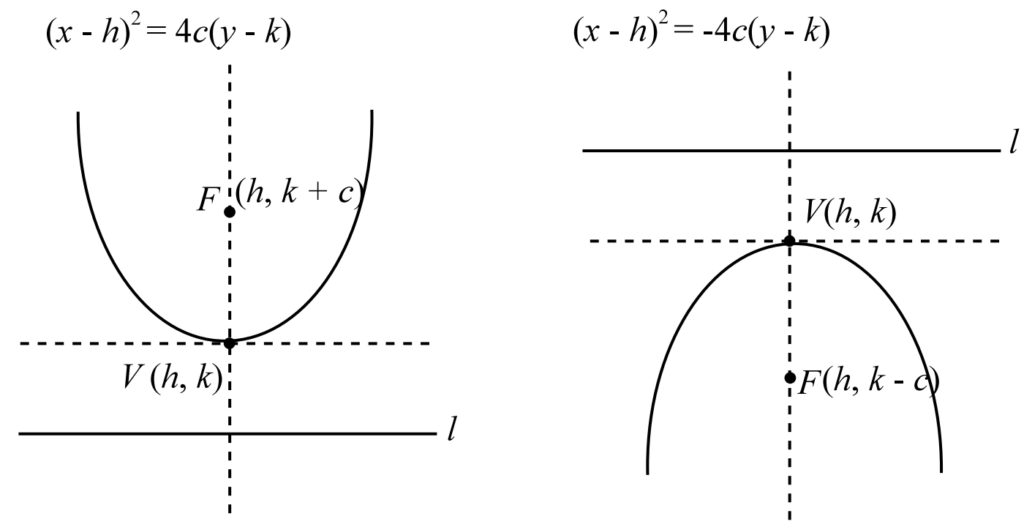
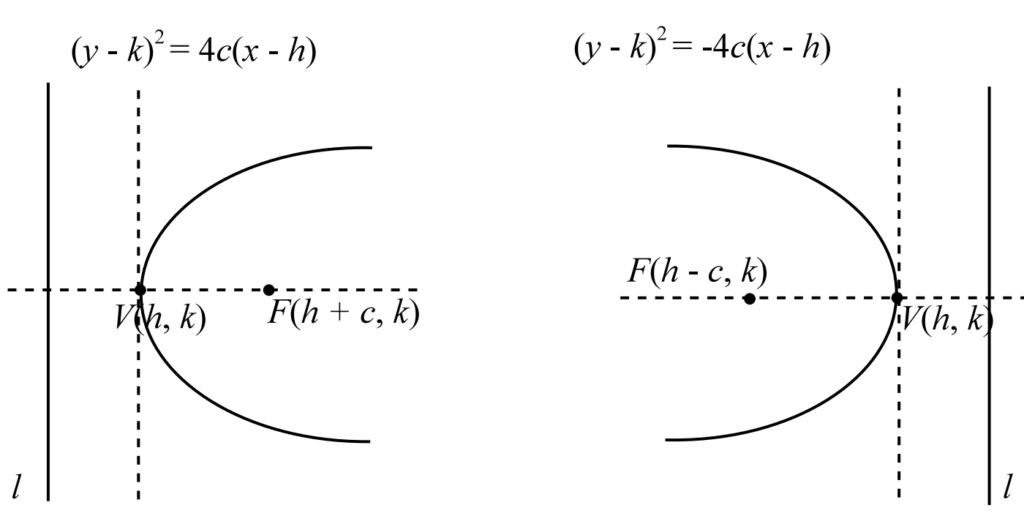
✨ตัวอย่างที่ 4 กำหนดสมการพาราโบลา y2–2y+8x–15=0 จงหาจุดยอดและจุดโฟกัสของพาราโบลานี้
✨วิธีทำ
ทำการจัดรูปสมการดังนี้
y2–2y+8x–15y2–2yy2–2y+1(y−1)2(y−1)2=0=−8x+15=−8x+15+1=−8x+16=−4(2)(x–2)
จากสมการ เราจึงสรุปได้ว่าจุดยอดของพาราโบลาคือ (2,1) และจุดโฟกัสคือ (2−2,1)=(0,1)
✨ไฮเพอร์โบลาโบลา
ไฮเพอร์โบลาโดยนิยามแล้วหมายถึงเซตของจุดทุกจุดบนระนาบซึ่งมีผลต่างของระยะทางจากจุดใด ๆ ไปยังจุดคงที่สองจุดมีค่าคงที่เสมอ โดยเราจะเรียกสองจุดนั้นว่าจุดโฟกัสของไฮเพอร์โบลา
✨ส่วนประกอบของไฮเพอร์โบลา
สิ่งที่เราต้องทราบในพาราโบลาคือ จุดศูนย์กลาง C(h,k) แกนตามขวางของไฮเพอร์โบลา มีความยาว 2a และแกนสังยุค มีความยาว 2b
✨สมการไฮเพอร์โบลา
ไฮเพอร์โบลาที่เราจะสนใจจะมีทั้งหมด 2 แบบครับ คือไฮเพอร์โบลาในแนวตั้ง และไฮเพอร์โบลาในแนวนอน ซึ่งจะมีสมการดังต่อไปนี้ครับ
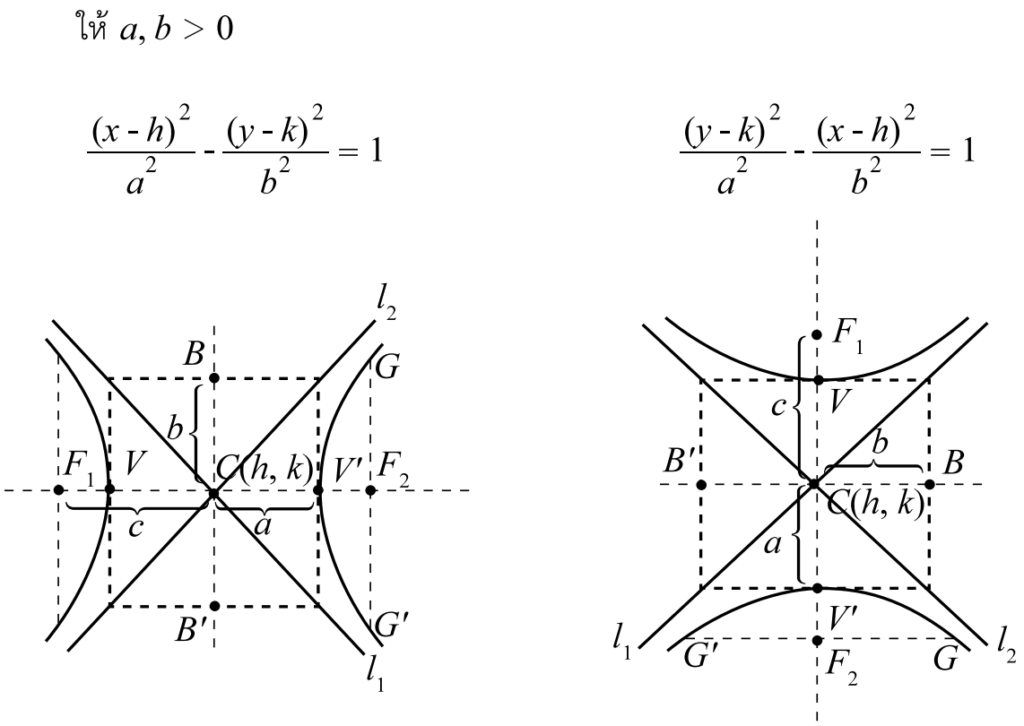
✨ตัวอย่างที่ 4 กำหนดสมการพาราโบลา y2–2y+8x–15=0 จงหาจุดยอดและจุดโฟกัสของพาราโบลานี้
✨วิธีทำ
ทำการจัดรูปสมการดังนี้
y2–2y+8x–15y2–2yy2–2y+1(y−1)2(y−1)2=0=−8x+15=−8x+15+1=−8x+16=−4(2)(x–2)
จากสมการ เราจึงสรุปได้ว่าจุดยอดของพาราโบลาคือ (2,1) และจุดโฟกัสคือ (2−2,1)=(0,1)
✨ข้อควรรู้เกี่ยวกับไฮเพอร์โบลา
- ผลต่างของระยะทางจากจุดใด ๆ บนไฮเพอร์โบลาไปยังจุดคงที่สองจุดมีค่าคงที่เสมอและเท่ากับ 2a
- c2=a2+b2 เสมอ
- แกนตามขวางยาว 2a แกนสังยุค 2b เลตัสเรกตัมยาว a2b2
✨ตัวอย่างที่ 5 กำหนดสมการไฮเพอร์โบลา 4y2–9x2–16y–54x–101=0 จงหาจุดศูนย์กลางของไฮเพอร์โบลานี้
✨วิธีทำ
ทำการจัดรูปสมการดังนี้
4y2–9x2–16y–54x–101(4y2–16y)–(9x2+54x)9(y2–4y)–4(x2+6x)9(y−2)2–4(x+3)29(y−2)2–4(x+3)2=0=101=36101=36101+94+49=1
จากสมการ เราจึงสรุปได้ว่าจุดศูนย์กลางของไฮเพอร์โบลาคือ (−3,2)
เป็นยังไงบ้างครับน้อง ๆ สำหรับเนื้อหา เรขาคณิตวิเคราะห์ และภาคตัดกรวย ที่พี่นำมาฝากในวันนี้ หวังว่าน้อง ๆ จะได้เข้าใจถึงความเชื่อมโยงระหว่างสมการและรูปต่าง ๆ มากขึ้น ไม่ว่าจะเป็นพาราโบลา วงรี ไฮเพอร์โบลา หรือแม้แต่วงกลม ทั้งหมดนี้จะช่วยทำให้เราเห็นความสัมพันธ์ที่ซ่อนอยู่ในรูปต่าง ๆ ครับ
อย่าลืมนะครับว่า การฝึกทำโจทย์บ่อย ๆ จะช่วยให้น้องเข้าใจเนื้อหาได้ลึกซึ้งยิ่งขึ้น พี่หวังว่าบทเรียนนี้จะเป็นพื้นฐานที่ดีให้น้อง ๆ นำไปต่อยอดในเรื่องอื่น ๆ ได้นะครับ ถ้าน้องๆ คิดว่าแค่อ่านบทความแล้วยังไม่พอ พี่ออนดีมานด์มีคอร์สเรียนแนะนำดีๆ มาบอกต่อ









