เมื่อพูดถึงแคลคูลัสน้อง ๆ หลายคนอาจจะกลัวบทนี้เพราะคิดว่าเป็นบทที่เข้าใจได้ยาก แต่จริง ๆ แล้วถ้าเราเข้าใจแนวคิดพื้นฐานของแต่ละสิ่งในแคลคูลัส เนื้อหาโดยรวมจะไม่ได้ยากอย่างที่น้อง ๆ คิดครับ อีกทั้งยังเป็นบทที่เราจะได้เรียนต่อในระดับมหาวิทยาลัยด้วย
สำหรับวันนี้พี่ได้เตรียมสรุปเนื้อหาแคลคูลัสมาให้น้อง ๆ ได้ลองอ่านกันครับ โดยจะประกอบด้วยเนื้อหาใหญ่ ๆ 3 ส่วนด้วยกันครับ ได้แก่ ลิมิตและความต่อเนื่อง อนุพันธ์ของฟังก์ชัน ปฏิยานุพันธ์ของฟังก์ชัน ถ้าน้อง ๆ พร้อมกันแล้ว ไปดูเนื้อหากันเลยย
ลิมิตและความต่อเนื่อง
ลิมิตของฟังก์ชัน
พิจารณากราฟของ f(x) = 2x+6
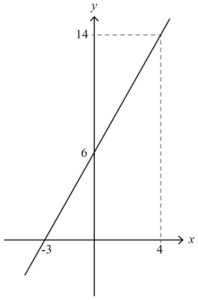
จากกราฟ เราจะพบว่า
- ▪️ เมื่อ x มีค่าเข้าใกล้ 4 ทางซ้าย จะเห็นว่าค่า y มีค่าเข้าใกล้ 14 จะได้ว่า 14 คือค่าลิมิตของ f(x) เมื่อ x มีค่าเข้าใกล้ 4 ทางซ้ายเขียนแทนด้วย \displaystyle \lim_{x \to 4^-} f(x) = 14
- ▪️ เมื่อ x มีค่าเข้าใกล้ 4 ทางขวา จะเห็นว่าค่า y มีค่าเข้าใกล้ 14 จะได้ว่า 14 คือค่าลิมิตของ f(x) เมื่อ x มีค่าเข้าใกล้ 4 ทางขวาเขียนแทนด้วย \displaystyle \lim_{x \to 4^+} f(x) = 14
- ▪️ เมื่อ x มีค่าเข้าใกล้ 4 ทั้งทางซ้ายและทางขวา จะเห็นว่าค่า y มีค่าเข้าใกล้ 14 เพียงค่าเดียว จะได้ว่า 14 คือค่าลิมิตของ f(x) เมื่อ x มีค่าเข้าใกล้ 4 เขียนแทนด้วย \displaystyle \lim_{x \to 4} f(x) = 14
โดยการพิจารณาเช่นนี้ เราจึงมีบทนิยามสำหรับลิมิตฟังก์ชันดังนี้ครับ

ทฤษฎีบทลิมิตเมื่อ x เข้าใกล้ a
ให้ \displaystyle \lim_{x \to a} f(x) = L, \lim_{x \to a} g(x) = M เมื่อ L, M เป็นจำนวนจริง เราจะได้ว่า
- \displaystyle \lim_{x \to a} k = k เมื่อ k เป็นค่าคงที่
- \displaystyle \lim_{x \to a} x = a
- ให้ m, n เป็นจำนวนเต็มบวกแล้ว \displaystyle \lim_{x \to a} x^{\frac{m}{n}} = a^{\frac{m}{n}} เมื่อ a^{\frac{m}{n}} เป็นจำนวนจริง
- \displaystyle \lim_{x \to a} kf(x) = k \lim_{x \to a} f(x) = kL เมื่อ k เป็นค่าคงที่
- \displaystyle \lim_{x \to a} (f(x) \pm g(x)) = \lim_{x \to a}f(x) \pm \lim_{x \ to a}g(x) = L \pm M
- \displaystyle \lim_{x \to a} (f(x) \cdot g(x)) = \lim_{x \to a}f(x) \cdot \lim_{x \ to a}g(x) = L \cdot M
- \lim_{x \to a}\left(\dfrac{f(x)}{g(x)}\right) = \dfrac{\lim_{x \to a}f(x)}{\lim_{x \to a}g(x)} = \dfrac{L}{M} เมื่อ M \neq 0
- \lim_{x \to a} |f(x)| = \left|\lim_{x \to a}f(x)\right| = |L|
- \lim_{x \to a}(f(x))^n = \left(\lim_{x \to a} f(x)\right)^n = L^n เมื่อ n เป็นจำนวนเต็มบวก
- \displaystyle \lim_{x \to a} \sqrt[n]{f(x)} = \sqrt[n]{\lim_{x \to a}f(x)} = \sqrt[n]{L} เมื่อ n เป็นจำนวนเต็มบวก และ \sqrt[n]{L} เป็นจำนวนจริง
หลักการหา \displaystyle \lim_{x \to a}\dfrac{f(x)}{g(x)}
เริ่มแรกให้เราแทน x = a ลงใน \dfrac{f(x)}{g(x)} ก่อนครับว่าได้ค่าออกมาเป็นยังไง
- ▪️ ถ้าเป็นตัวเลขก็ตอบค่านั้นได้เลย
- ▪️ ถ้าเป็น \dfrac{0}{0} ต้องจัดรูปต่อโดยการแยกตัวประกอบหรือใช้คอนจูเกต
- ▪️ ถ้าตัวส่วนเป็น 0 จะได้ว่าไม่มีลิมิต
ตัวอย่างที่ 1 จงหา \displaystyle \lim_{x \to 2} \dfrac{x^2 – 4}{x-2}
วิธีทำ
จากโจทย์ถ้าแราแทนค่า x = 2 ลงไปเลย จะพบว่าค่าที่ได้จะเป็น \dfrac{0}{0} ดังนั้นเราจึงทำต่อโดยการแยกตัวประกอบได้เป็น \displaystyle \lim_{x \to 2} \dfrac{(x-2)(x+2)}{x-2} แล้วจะสามารถตัดทอนได้เป็น \displaystyle \lim_{x \to 2} x+2 เมื่อแทนค่าอีกครั้ง จะได้ค่าของลิมิตเท่ากับ 2+2 = 4 นั่นเอง
ความต่อเนื่องของฟังก์ชัน
มีหลักการตรวจสอบว่าฟังก์ชัน f ต่อเนื่องที่ x = a ดังนี้
- f(a) หาค่าได้
- \displaystyle \lim_{x \to a}f(x) หาค่าได้ \displaystyle \left(\lim_{x \to a^-}f(x) = \lim_{x \to a^+}f(x)\right)
- \displaystyle f(a) = \lim_{x \to a}f(x)
ถ้าขาดสมบัติข้อใดข้อหนึ่งไป เราจะถือว่า f ไม่ต่อเนื่องที่ x = a ครับ
ตัวอย่างที่ 2 กำหนดให้ \displaystyle f(x) = \begin{cases}x^2 &, x \geqslant 0 \\x &, x < 0\end{cases}
จงพิจารณาว่า f เป็นฟังก์ชันต่อเนื่องที่ x = 0 หรือไม่
วิธีทำ
เราจะทำการตรวบสอบสมบัติแต่ละข้อตามหลักการตรวจสอบก่อนหน้า ดังนี้ครับ
- f(0) = 0^2 = 0 นั่นคือ f(0) หาค่าได้
- \displaystyle \lim_{x \to 0^-}f(x) = 0, \displaystyle \lim_{x \to 0^+}f(x) = 0^2 = 0 นั่นคือ \displaystyle \lim_{x \to a}f(x) หาค่าได้
- พบว่า \displaystyle f(0) = \lim_{x \to 0}f(x)
เราจึงสามารถสรุปได้ว่า f เป็นฟังก์ชันต่อเนื่องที่ x = 0
อนุพันธ์ของฟังก์ชัน
อัตราการเปลี่ยนแปลงเฉลี่ยของ y เทียบกับ x จาก x ถึง x+h
คือ \dfrac{\Delta y}{\Delta x} = \dfrac{f(x+h) – f(x)}{x+h-x} = \dfrac{f(x+h) – f(x)}{h}
อัตราการเปลี่ยนแปลงของ y เทียบกับ x ขณะ x มีค่าใด ๆ
คือ \displaystyle \lim_{h \to 0}\dfrac{f(x+h) – f(x)}{h} (ช่วงที่ x เปลี่ยนแปลงน้อยมาก ๆ)
เราจะเรียก \displaystyle \lim_{h \to 0}\dfrac{f(x+h) – f(x)}{h} ว่า อนุพันธ์ของฟังก์ชัน f และจะใช้สัญลักษณ์ f’(x), y’, \dfrac{dy}{dx}, \dfrac{df}{dx} แทนอนุพันธ์ของฟังก์ชัน f[/katex</span></p><p><b>การหาอนุพันธ์โดยใช้สูตร</b></p><p><span style="font-weight: 400;">ให้ k เป็นค่าคงตัว เราจะได้ว่า
- \dfrac{d}{dx}k = 0
- \dfrac{d}{dx}kx^n = k\dfrac{d}{dx}x^n
- \dfrac{d}{dx}x^n = nx^{n-1}
- \dfrac{d}{dx}(u \pm v) = u’ \pm v’
- \dfrac{d}{dx}(uv) = uv’ + vu’
- \dfrac{d}{dx}\left(\dfrac{u}{v}\right) = \dfrac{vu’ - uv’}{v^2}
ตัวอย่างที่ 3 จงหาอนุพันธ์ของ f(x) = (x^2-3)(3x+4)
วิธีทำ
\begin{aligned}f(x) &= (x^2-3)(3x+4) \\f’(x) &= (x^2-3)\dfrac{d}{dx}(3x+4) + (3x+4)\dfrac{d}{dx}(x^2-3) \\f’(x) &= (x^2-3)(3) + (3x+4)(2x) \\f’(x) &= 3x^2-9+6x^2+4x \\f’(x) &= 9x^2+4x-9\end{aligned}
การหาอนุพันธ์ของฟังก์ชันประกอบ
ถ้า f, g เป็นฟังก์ชัน เราจะได้ว่า (g \circ f)’(x) = g’(f(x)) \cdot f’(x)
ตัวอย่างที่ 4 จงหาอนุพันธ์ของ f(x) = (3x+2)^3
วิธีทำ
\begin{aligned}f(x) &= (3x+2)^3 \\f’(x) &= 3(3x+2)^2 \dfrac{d}{dx}(3x+2) \\f’(x) &= 3(3x+2)^2 (3) \\f’(x) &= 9(3x+2)^2 \\\end{aligned}
อนุพันธ์อันดับสูง
คือการหาอนุพันธ์มากกว่าหนึ่งครั้ง
f’(x) คืออนุพันธ์ของ f
f’’(x) คืออนุพันธ์ของ f’(x) หรืออนุพันธ์อันดับสองของ f
f’’’(x) คืออนุพันธ์ของ f’’(x) หรืออนุพันธ์อันดับสามของ f
f^{(4)}(x) คืออนุพันธ์ของ f’’’(x) หรืออนุพันธ์อันดับสี่ของ f
ตัวอย่างที่ 5 จงหาอนุพันธ์อันดับสามของ f(x) = (x^2-3)(3x+4)
วิธีทำ
\begin{aligned}f(x) &= (x^2-3)(3x+4) \\f’(x) &= (x^2-3)\dfrac{d}{dx}(3x+4) + (3x+4)\dfrac{d}{dx}(x^2-3) \\f’(x) &= (x^2-3)(3) + (3x+4)(2x) \\f’(x) &= 3x^2-9+6x^2+4x \\f’(x) &= 9x^2+4x-9 \\f’’(x) &= 18x + 4 \\f’’’(x) &= 18\end{aligned}
ปฏิยานุพันธ์
ความหมายของปฏิยานุพันธ์
ฟังก์ชัน F(x) เป็นปฏิยานุพันธ์หนึ่งของ f(x) ก็ต่อเมื่อ F’(x) = f(x)
เช่น x^2 เป็นปฏิยานุพันธ์หนึ่งของ 2x เพราะ \dfrac{d}{dx}(x^2) = 2x
x^2 + 4 เป็นปฏิยานุพันธ์หนึ่งของ 2x เพราะ \dfrac{d}{dx}(x^2+4) = 2x
f(x) เป็นปฏิยานุพันธ์หนึ่งของ f’(x) เพราะ \dfrac{d}{dx}f(x) = f’(x)
เราจะเรียกปฏิยานุพันธ์ทั่วไปของ f ว่า อินทิกรัลไม่จำกัดเขตของ f และจะแทนปฏิยานุพันธ์ทั่วไปของ f ด้วยสัญลักษณ์ \displaystyle \in f(x) \, dx หรือ \displaystyle F(x) =\int f(x) \, dx
สูตรการหาอินทิกรัลไม่จำกัดเขตของ f
ให้ k และ c เป็นค่าคงตัว
- \displaystyle \int k \, dx = kx + c
- \displaystyle \int x^n \, dx = \dfrac{x^{n+1}}{n+1} + c, n \neq -1
- \displaystyle \int kf(x) \, dx = k \int f(x) \, dx
- \displaystyle \int f(x) \pm g(x) \, dx = \int f(x) \, dx \pm \int g(x) \, dx
- \displaystyle \int f’(x) \, dx = f(x) + c
ตัวอย่างที่ 6 จงหา \displaystyle \int (4x^3 + 2x+1) \, dx
วิธีทำ
\begin{aligned}\int (4x^3 + 2x+1) \, dx &= \dfrac{4x^4}{4} + \dfrac{2x^2}{2} + x + c \\\int (4x^3 + 2x+1) \, dx &= x^4 + x^2 + x + c \\\end{aligned}
นั่นคือ \displaystyle \int (4x^3 + 2x+1) \, dx = x^4 + x^2 + x + c
การหาอินทิกรัลจำกัดเขต
ถ้า F(x) เป็นปฏิยานุพันธ์ของ f(x) จะได้ว่า \displaystyle \int_a^b f(x) \, dx = F(b) – F(a)
ตัวอย่างที่ 7 จงหา \displaystyle \int_0^1 (4x^3 + 2x+1) \, dx
วิธีทำ
ขั้นแรกเราจะหาอินทิกรัลไม่จำกัดเขตก่อน
\begin{aligned}\int (4x^3 + 2x+1) \, dx &= \dfrac{4x^4}{4} + \dfrac{2x^2}{2} + x + c \\\int (4x^3 + 2x+1) \, dx &= x^4 + x^2 + x + c \\\end{aligned}
ต่อไปเราจะนำค่าขอบเขตไปแทน ดังนี้
\begin{aligned}\int (4x^3 + 2x+1) \, dx &= x^4 + x^2 + x + c \\\int_0^1 (4x^3 + 2x+1) \, dx &= (1^4 + 1^2 + 1 + c) – (0^4 + 0^2 + 0 + c) \\&= (1+1+1+c) – (0+0+0+c) \\&= 3+c-0-c \\&= 3\end{aligned}
นั่นคือ \displaystyle \int_0^1 (4x^3 + 2x+1) \, dx = 3
การประยุกต์ของอนุพันธ์และปฏิยานุพันธ์
การประยุกต์ของอนุพันธ์ – ความชันเส้นสัมผัส (ความชันเส้นโค้ง)
y = f(x) เป็นสมการเส้นโค้ง ดังรูป
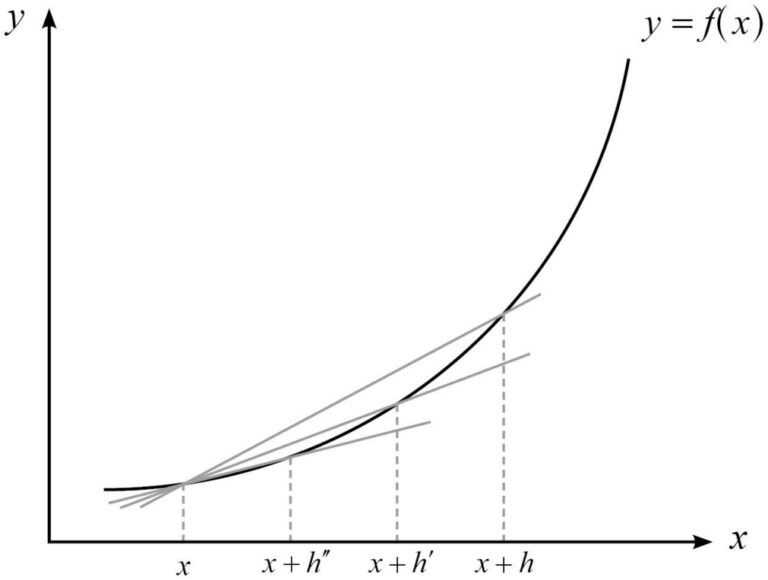
เราจะได้ว่าความชันของเส้นตรงที่สัมผัสเส้นโค้งที่จุด (x, y) ใด ๆ มีค่าเท่ากับ \displaystyle \lim_{h \to 0} \dfrac{f(x+h) – f(x)}{h} หรือก็คือ ความชันของเส้นตรงที่สัมผัสเส้นโค้งจะหาได้จาก f’(x) นั่นเอง

การประยุกต์ของอนุพันธ์ – ฟังก์ชันเพิ่ม ฟังก์ชันลด
พิจารณาช่วงที่ f เป็นฟังก์ชันเพิ่ม
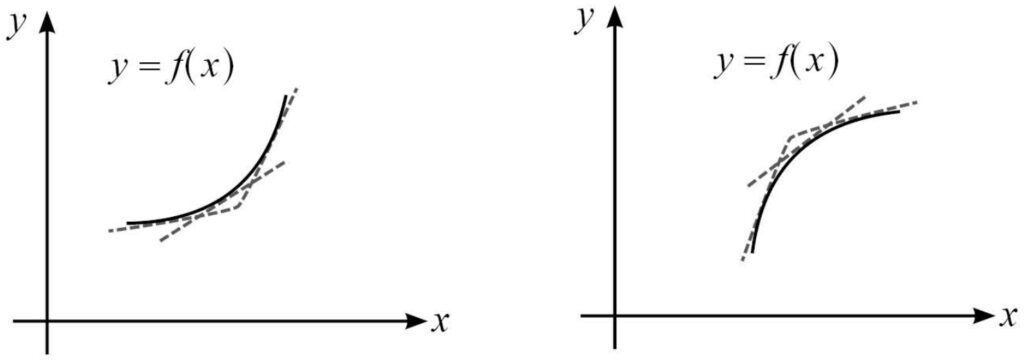
จะเห็นว่าช่วงที่ f เป็นฟังก์ชันเพิ่มคือช่วงที่ f มีค่าความชันเส้นสัมผัสเป็นบวก
พิจารณาช่วงที่ f เป็นฟังก์ชันลด
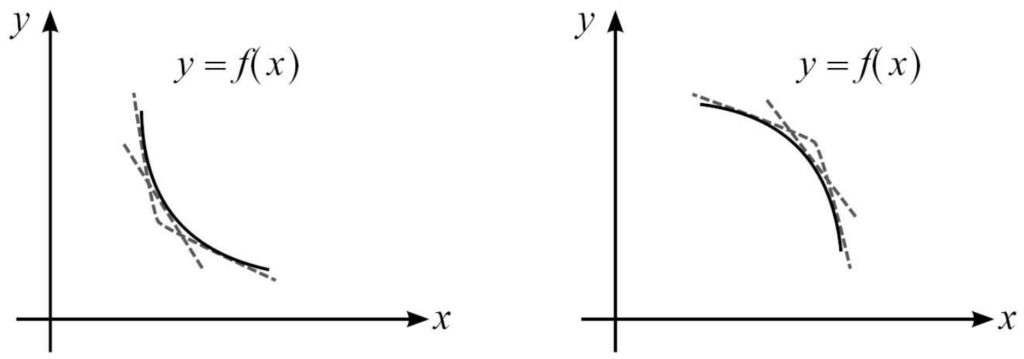
จะเห็นว่าช่วงที่ f เป็นฟังก์ชันลดคือช่วงที่ f มีค่าความชันเส้นสัมผัสเป็นบลบ
การประยุกต์ของอนุพันธ์ – จุดสูงสุดสัมพัทธ์ จุดต่ำสุดสัมพัทธ์
พิจารณากราฟ
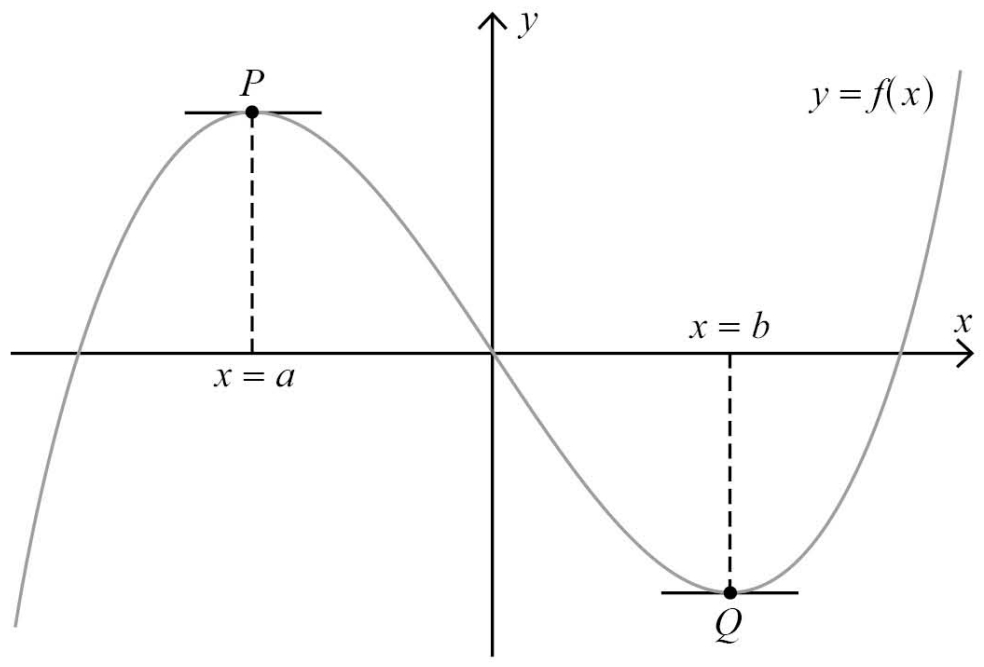
จากรูป เราจะเรียกจุด P ว่าจุดสูงสุดสัมพัทธ์
และเรียกจุด Q ว่าจุดต่ำสุดสัมพัทธ์
หรือจะพูดให้เข้าใจง่าย ๆ ก็คือ จุดสูงสุดสัมพัทธ์ก็คือจุดที่อยู่สูงที่สุดเมื่อเทียบกับจุดอื่นใกล้ ๆ กับตัวมันเอง และจุดต่ำสุดสัมพัทธ์ก็คือจุดที่อยู่ต่ำที่สุดเมื่อเทียบกับจุดอื่นใกล้ ๆ กับตัวมันเองนั่นเองครับ
หลักการหาจุดสูงสุดสัมพัทธ์ จุดต่ำสุดสัมพัทธ์
- หาค่า x ที่ทำให้ f’(x) = 0 หรือหาค่าไม่ได้ เราจะเรียกค่า x ที่ได้มานั้นว่า ค่าวิกฤต
- ทดสอบว่าค่าวิกฤตที่ได้นั้น (สมมุติว่าเป็น c) ให้จุดสูงสุดสัมพัทธ์หรือจุดต่ำสุดสัมพัทธ์
2.1 ถ้าความชันเส้นสัมผัสเปลี่ยนจาก + ไป – จะได้ว่าที่ x = c จะให้จุดสูงสุดสัมพัทธ์
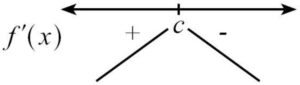
2.2 ถ้าความชันเส้นสัมผัสเปลี่ยนจาก – ไป + จะได้ว่าที่ x = c จะให้จุดต่ำสุดสัมพัทธ์
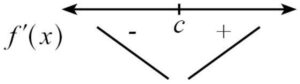
2.3 แต่ถ้าความชันเส้นสัมผัสไม่เปลี่ยน จะได้ว่าที่ x = c จะให้จุดเปลี่ยนเว้า
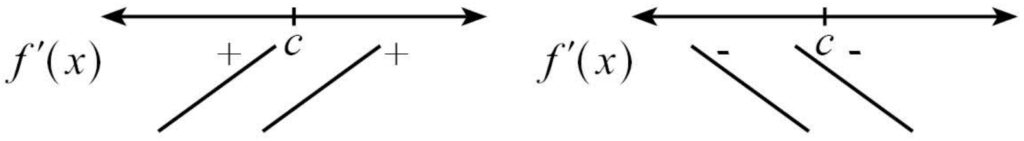
การประยุกต์ของอนุพันธ์ – จุดสูงสุดสัมบูรณ์ จุดต่ำสุดสัมบูรณ์
พิจารณากราฟในช่วง a, b
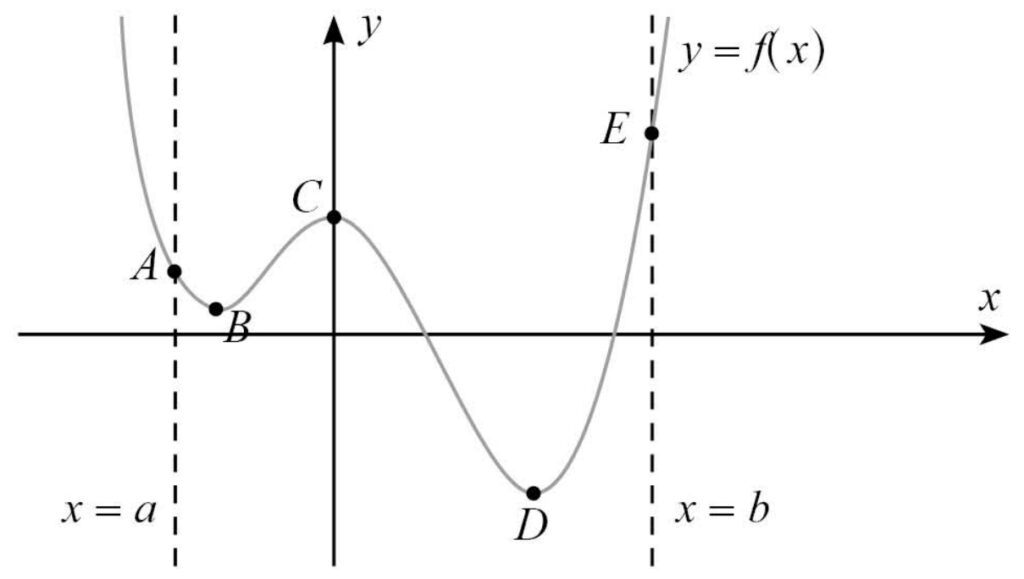
จากรูป เราจะเรียกจุด E ว่าจุดสูงสุดสัมบูรณ์
และเรียกจุด D ว่าจุดต่ำสุดสัมบูรณ์
หรือจะพูดให้เข้าใจง่าย ๆ ก็คือ จุดสูงสุดสัมบูรณ์ก็คือจุดที่อยู่สูงที่สุดของกราฟในช่วงที่เรากำลังพิจารณา และจุดต่ำสุดสัมบูรณ์ก็คือจุดที่อยู่ต่ำที่สุดของกราฟในช่วงที่เรากำลังพิจารณานั่นเองครับ
หลักการหาจุดสูงสุดสัมบูรณ์ จุดต่ำสุดสัมบูรณ์ ในช่วง [a, b]
- หาค่า x ที่ทำให้ f’(x) = 0 หรือหาค่าไม่ได้ เราจะเรียกค่า x ที่ได้มานั้นว่า ค่าวิกฤต
- พิจารณาค่าวิกฤตในช่วง [a, b]
- เปรียบเทียบค่า y ของค่าวิกฤตกับจุดปลายช่วง
สมมุติได้ค่าวิกฤตที่อยู่ในช่วง [a, b] คือ x = c, d
เปรียบเทียบ f(a), f(b), f(c), f(d)
ค่าสูงสุดสัมบูรณ์คือค่า y ของจุดสูงสุดสัมบูรณ์
ค่าต่ำสุดสัมบูรณ์คือค่า y ของจุดต่ำสุดสัมบูรณ์
การประยุกต์ของปฏิยานุพันธ์ – พื้นที่ใต้เส้นโค้ง
ทฤษฎีบท กำหนดให้ฟังก์ชัน f ต่อเนื่องบน [a, b] และ A เป็นพื้นที่ปิดล้อมด้วยเส้นโค้งของ f จาก x = a ถึง x = b จะได้ว่า
- ▪️ ถ้า f(x) \geqslant 0 สำหรับทุก x ในช่วง [a, b] แล้ว \displaystyle A = \int_a^b f(x) \, dx
- ▪️ ถ้า f(x) \leqslant 0 สำหรับทุก x ในช่วง [a, b] แล้ว \displaystyle A = -\int_a^b f(x) \, dx
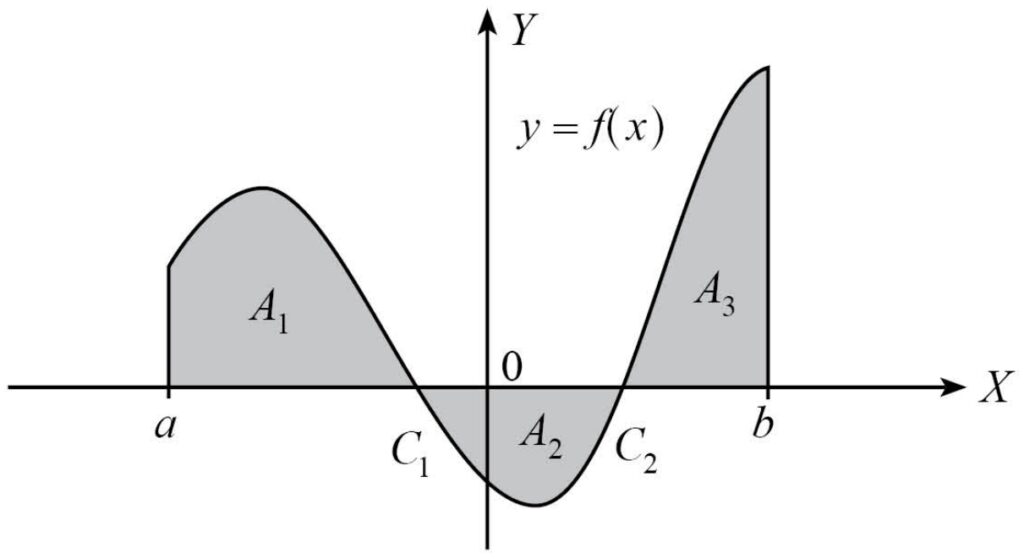
หลักการหาพื้นที่ใต้เส้นโค้งกับแกน X ในช่วง [a, b]
- วาดกราฟคร่าว ๆ
- หาค่าสัมบูรณ์ของอินทิกรัลจำกัดเขตในแต่ละช่วงของ x
- พื้นที่ที่ต้องการเท่ากับผลรวมของค่าสัมบูรณ์ของอินทิกรัลจำกัดเขตทั้งหมดที่หาได้
เป็นยังไงกันบ้างครับ สำหรับเนื้อหาเรื่องแคลคูลัสที่พี่นำมาฝากน้อง ๆ ทุกคนในวันนี้ น้อง ๆ หลายคนอาจจะอ่านแล้วยังไม่เข้าใจในทันที แต่เราไม่จำเป็นต้องเข้าใจเนื้อหาทั้งหมดนี้ภายในวันเดียวหรือการอ่านเพียงรอบเดียวก็ได้ครับ เราสามารถค่อย ๆ ทบทวนเนื้อหาไปพร้อมกับการฝึกทำโจทย์เพื่อให้เก่งขึ้นได้
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์