สวัสดีน้อง ๆ ทุกคนครับ! วันนี้พี่จะพาน้อง ๆ ไปรู้จักกับรูปเรขาคณิตชนิดหนึ่งซึ่งเป็นรูปที่น่าสนใจและมีความสำคัญมากในวิชาคณิตศาสตร์ รูปนั้นก็คือรูปวงกลมนั่นเองครับ เพราะวงกลมนั้นมีทฤษฎีบทที่สามารถนำไปประยุกต์ใช้ในการแก้ปัญหาทางเรขาคณิตได้หลายทฤษฎีบท ถ้าน้อง ๆ พร้อมแล้ว ไปดูเนื้อหากันเลยยย
ส่วนประกอบของวงกลม
ก่อนที่เราจะไปถึงเนื้อหาที่เกี่ยวกับทฤษฎีบทของวงกลม เราจะต้องรู้จักส่วนประกอบต่าง ๆ ของวงกลมก่อนนะครับ พี่สรุปให้เป็นรูปภาพแบบเข้าใจง่าย ๆ ดังนี้ครับ

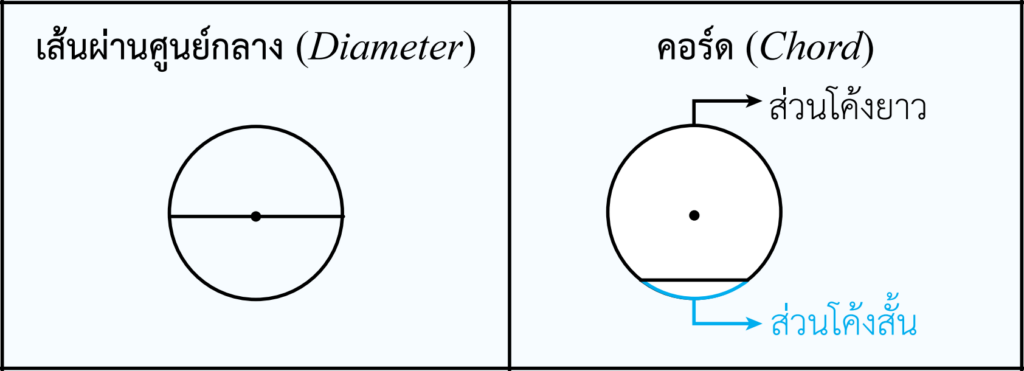
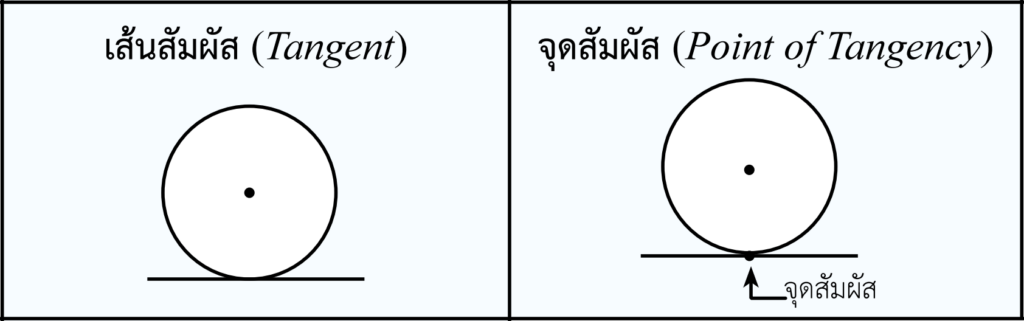
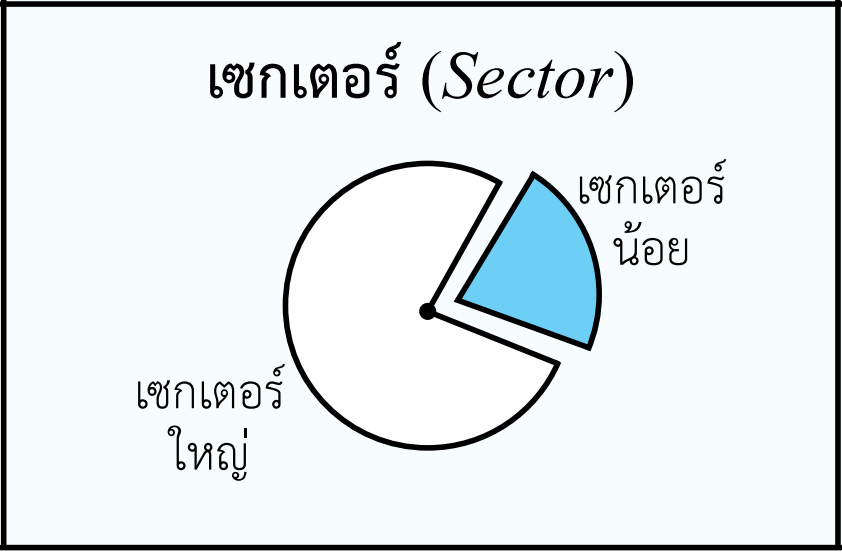
นอกจากนี้ก็ยังมีคำศัพท์ที่เอาไว้บอกตำแหน่งของมุมที่เกิดขึ้นภายในวงกลมกับส่วนโค้งด้วยครับ
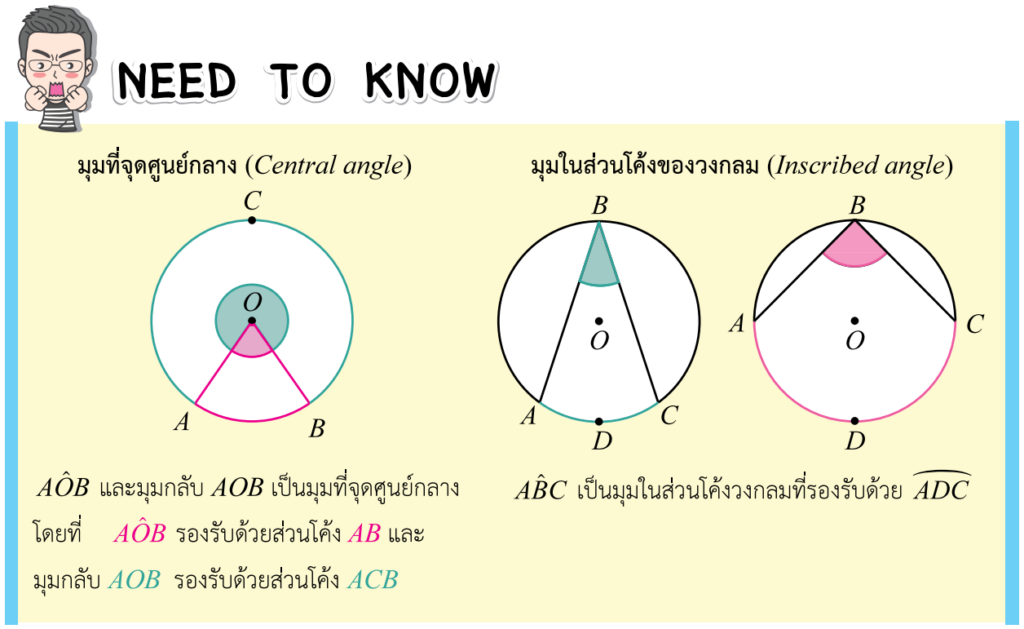
หลังจากน้อง ๆ ได้รู้จักกับส่วนประกอบต่าง ๆ ของวงกลม และมุมที่จุดศูนย์กลางกับมุมในส่วนโค้งของวงกลมไปแล้ว ต่อไปเรามาลองทำโจทย์ทดสอบความเข้าใจกันดูนะครับ
ตัวอย่างที่ 1 จากรูปที่กำหนดให้ มุมที่จุดศูนย์กลาง และมุมในส่วนโค้งวงกลม ได้แก่มุมใดบ้าง
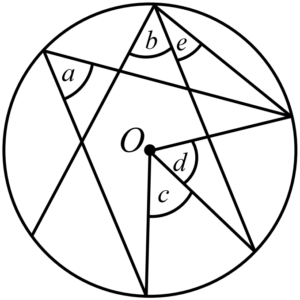
จากรูปที่โจทย์กำหนดให้ เราจะได้ว่า
มุมที่จุดศูนย์กลาง ได้แก่มุม c, d
มุมในส่วนโค้งวงกลม ได้แก่มุม a, b, e
ทฤษฎีบทวงกลม
พี่จะขอแบ่งทฤษฎีบทวงกลมออกเป็น 3 ส่วนดังนี้ครับ คือ
- ทฤษฎบทเกี่ยวกับมุมบนส่วนโค้ง และมุมที่จุดศูนย์กลาง
- ทฤษฎบทเกี่ยวกับคอร์ด
- ทฤษฎบทเกี่ยวกับเส้นสัมผัส
ไปดูทีละหัวข้อกันเลยครับ
ทฤษฎบทเกี่ยวกับมุมบนส่วนโค้ง และมุมที่จุดศูนย์กลาง
ประกอบด้วย 5 ทฤษฎีบทดังนี้ครับ

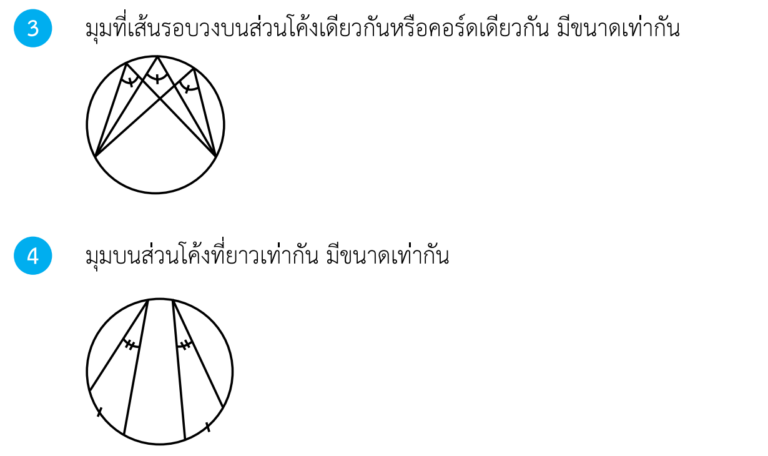

มาลองทำโจทย์ทดสอบความเข้าใจกันดูนะครับ
ตัวอย่างที่ 2 จงหาค่าของมุม a
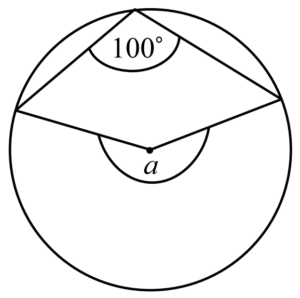
จากรูปเราพบว่ามุม 100^\circ กับมุม a เป็นมุมที่รองรับด้วยส่วนโค้งเดียวกัน โดยที่มุม 100^\circ เป็นมุมที่เส้นรอบวงของวงกลม แต่มุม a เป็นมุมที่จุดศูนย์กลาง ดังนั้นโดยทฤษฎีบทที่ 2 เราจึงทราบว่า a = 2(100^\circ) = 200^\circ นั่นเอง
ตัวอย่างที่ 3 จงหาค่าของมุม a
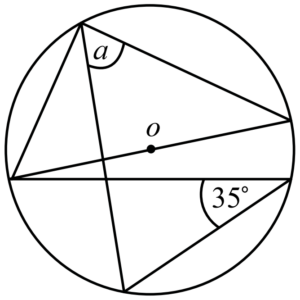
จากทฤษฎีบทที่ 3 เราจะได้ว่า b = 35^\circ
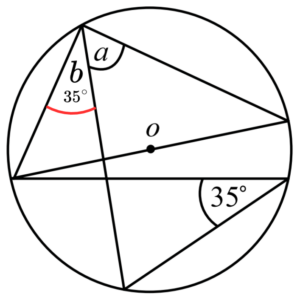
จากนั้นโดยทฤษฎีบทที่ 1 ทำให้เราทราบว่า a + b = 90^\circ
ดังนั้นเมื่อแทนค่า b = 35^\circ ลงในสมการข้างต้น เราจึงสรุปได้ว่ามุม a = 55^\circ นั่นเอง
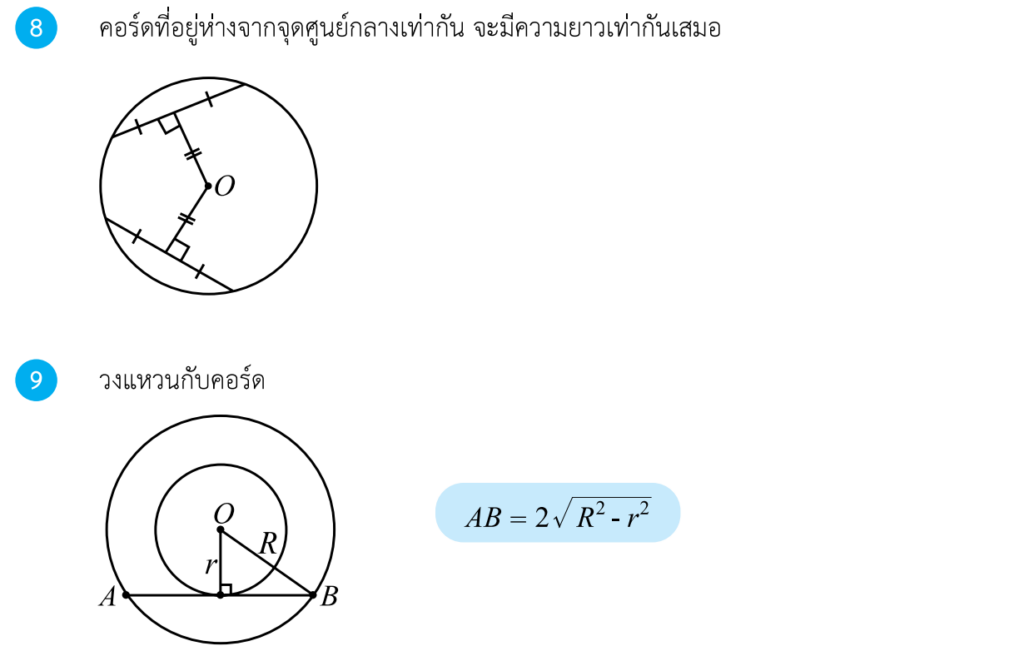
ทฤษฎีบทเกี่ยวกับคอร์ด
ประกอบด้วย 4 ทฤษฎีบทดังนี้ครับ
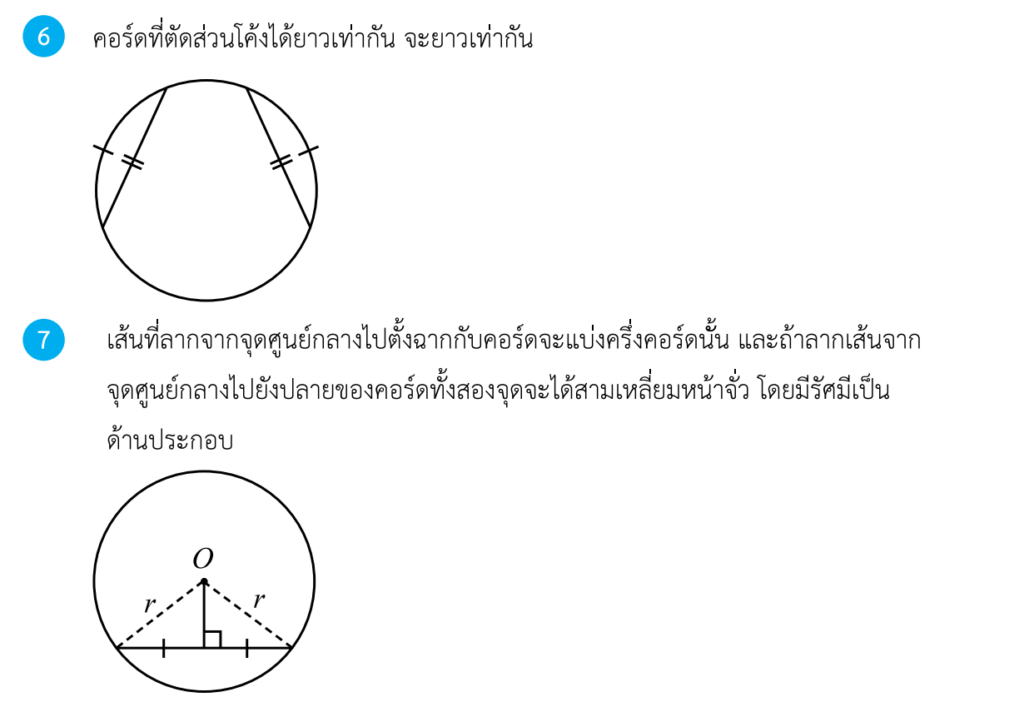
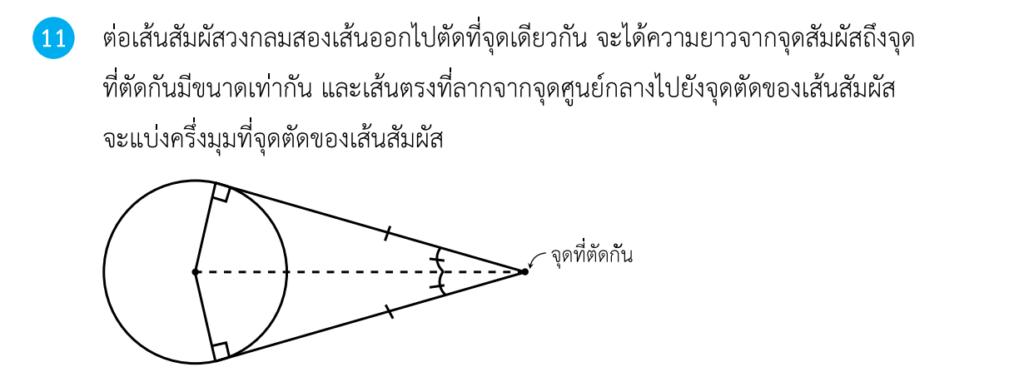
ทฤษฎีบทเกี่ยวกับเส้นสัมผัส
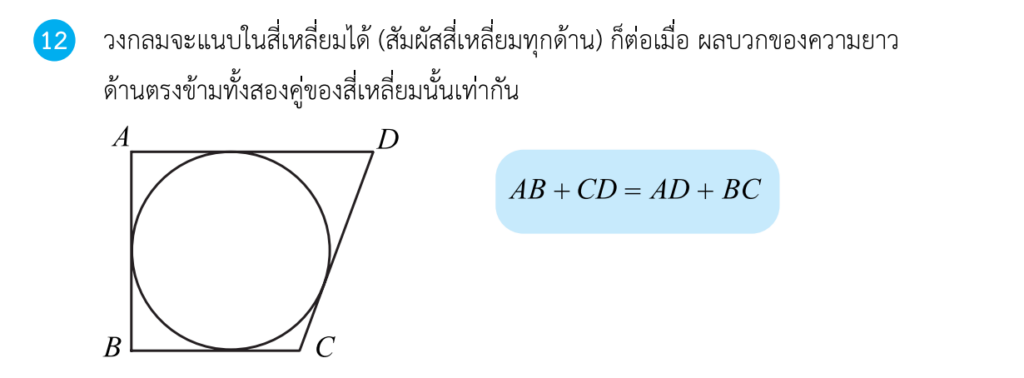
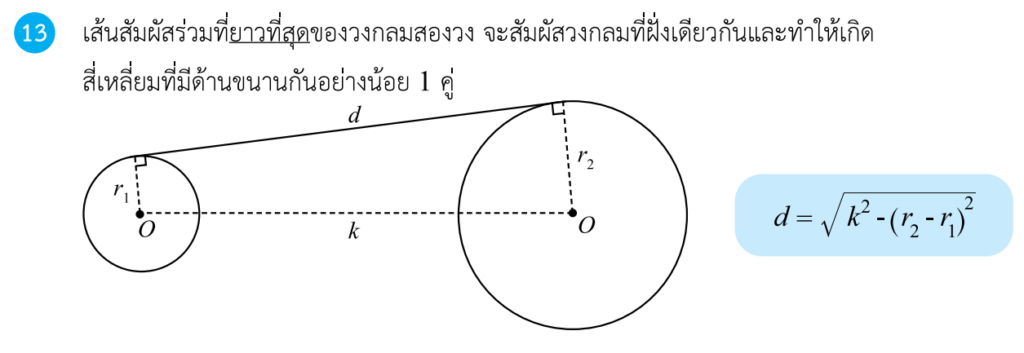
ประกอบด้วย 5 ทฤษฎีบทดังนี้ครับ

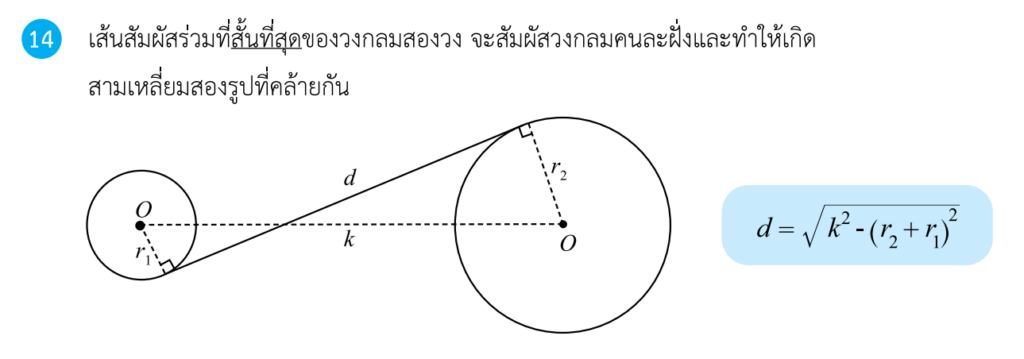
ตัวอย่างที่ 4 จงหาค่าของมุม a
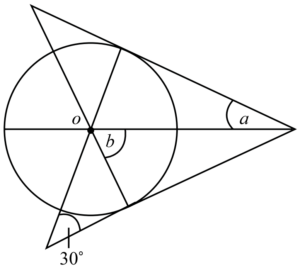
จากทฤษฎีบทที่ 5 เราจะได้ว่า c = 90^\circ
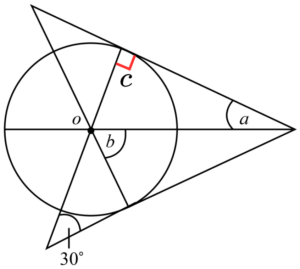
จากทฤษฎีบทที่ 11 เราจะได้ว่ามุมที่ติดกับมุม a ก็มีขนาดเท่ากับมุม a ด้วย
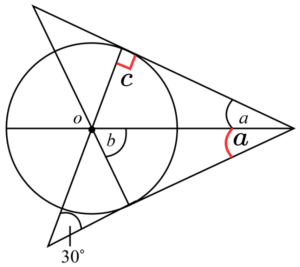
จากนั้นเราจะได้ว่า 30^\circ + c + 2a = 180^\circ เพราะเป็นมุมภายในรูปสามเหลี่ยม
ทำการแทนค่ามุม จะได้ 30^\circ + 90^\circ + 2a = 180^\circ
120^\circ + 2a = 180^\circ
2a = 60^\circ
เราจึงสรุปได้ว่า a = 30^\circ นั่นเอง
ตัวอย่างที่ 5 จงหาค่าของมุม a
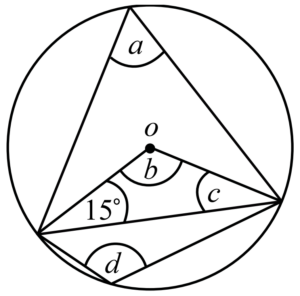
จากรูป เราจะทราบได้ทันทีว่า c = 15^\circ เพราะเป็นมุมที่ฐานของสามเหลี่ยมหน้าจั่ว
จากนั้นเราจะได้ว่า b = 180^\circ – 15^\circ – 15^\circ = 150^\circ เพราะเป็นมุมภายในสามเหลี่ยม
จากทฤษฎีบทที่ 2 เราจะได้ว่า 150^\circ = b = 2a
จึงทำให้เราสรุปได้ว่าa = 75^\circ นั่นเอง
เป็นยังไงบ้างครับน้อง ๆ สำหรับเนื้อหาวงกลมที่พี่นำมาฝากในวันนี้ หวังว่าน้อง ๆ จะได้เข้าใจถึงความเชื่อมโยงระหว่างส่วนประกอบต่าง ๆ ของวงกลมและทฤษฎีบทของวงกลมมากขึ้นครับ
อย่าลืมนะครับว่า การฝึกทำโจทย์บ่อย ๆ จะช่วยให้น้องเข้าใจเนื้อหาได้ลึกซึ้งยิ่งขึ้น พี่หวังว่าบทเรียนนี้จะเป็นพื้นฐานที่ดีให้น้อง ๆ นำไปต่อยอดในเรื่องอื่น ๆ ได้นะครับ
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand