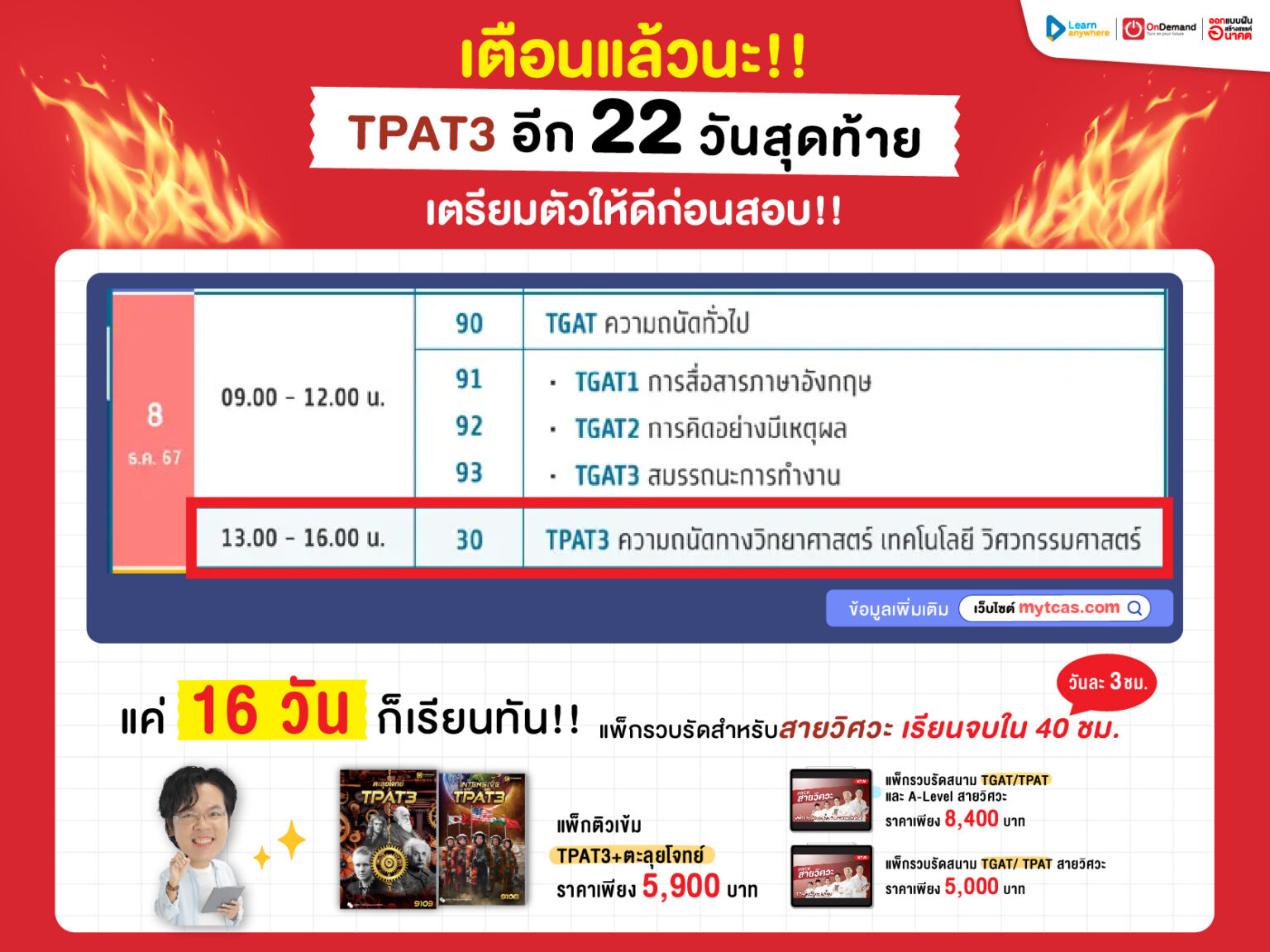
มีใครรู้สึกเหมือนกันบ้างมั้ยครับว่าพอขึ้น ม.5 แล้วเนื้อหา คณิตศาสตร์ ยิ่งซับซ้อนกว่าเดิม จนทำให้น้อง ๆ หลายคนเริ่มกังวลว่าจะตามเนื้อหาไม่ทัน ถ้าใครกำลังรู้สึกแบบนี้อยู่ ไม่ต้องกังวลไปนะ! วันนี้พี่ ออนดีมานด์ จะมาสรุปเนื้อหาสำคัญจากในเรื่อง เมทริกซ์ ให้ เข้าใจได้อย่างง่าย ๆ และไม่ซับซ้อน
ประโยชน์ของเมทริกซ์นั้นมีหลายอย่างมากครับ เช่น เราสามารถใช้เมทริกซ์มาช่วยแก้ระบบสมการเชิงเส้นหลาย ๆ ตัวแปรได้ เพราะเมทริกซ์จะทำให้กระบวนการแก้ระบบสมการของเรามีระเบียบแบบแผนมาก ทำให้ไม่สับสน หรือเราสามารถใช้ เมทริกซ์ ในการบันทึกข้อมูลต่าง ๆ ให้เป็นระเบียบก็ทำได้เช่นกัน ดังนั้นวันนี้พี่จึงจะมาสรุปเนื้อหาที่สำคัญในเรื่องเมทริกซ์ให้น้อง ๆ ครับ ไปเริ่มกันเลยยย
✨ความหมายของ เมทริกซ์
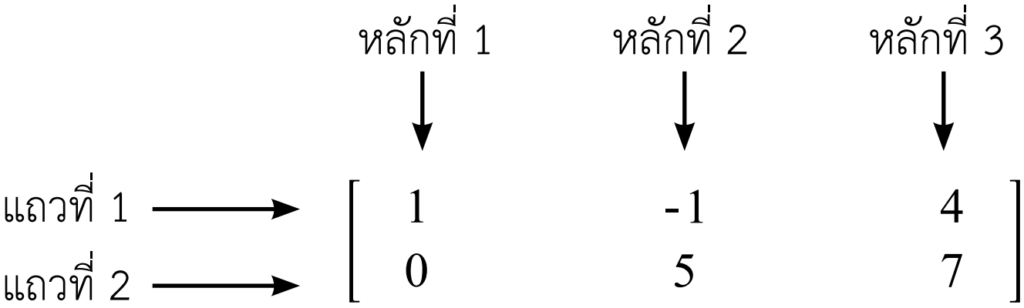
ก่อนอื่นเลย เมทริกซ์ (Matrix) ก็คือกลุ่มของจำนวนที่วางเรียงอยู่เป็นแถว (row) และหลัก (column) ซึ่งตัวเลขแต่ละตัวในเมทริกซ์เรียกว่า “สมาชิก” (elements) ของเมทริกซ์ โดยที่แต่ละแถวจะมีจำนวนเท่า ๆ กัน และถูกครอบด้วยเครื่องหมาย [ ] หรือ ( ) ก็ได้ครับ และต่อไปนี้คือตัวอย่างของเมทริกซ์ที่มีขนาดต่าง ๆ ครับ
\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix}, \begin{bmatrix} -1 & 0 & 1 \end{bmatrix}, \begin{pmatrix} 2 \\ 4 \end{pmatrix}
เพื่อให้เห็นภาพมากขึ้น น้อง ๆ สามารถดูรูปด้านล่างนี้เพื่อทำความเข้าใจเพิ่มเติมได้เลยครับ
✨ความรู้เบื้องต้นของ เมทริกซ์
ก่อนที่เราจะเข้าสู่เนื้อหา เราต้องทำข้อตกลงกันก่อน ดังนี้ครับ
ข้อตกลง
- เราจะเรียกเมทริกซ์ที่มี m แถว n หลักว่า “เมทริกซ์ขนาด m ]times n” หรือ “เมทริกซ์มิติ m ]times n” และเรียก m \times n ว่ามิติหรือขนาดของเมทริกซ์
- ใช้อักษรภาษาอังกฤษตัวพิมใหญ่แทนเมทริกซ์ เช่น A, B, C
- ใช้สัญลักษณ์ a_{ij} แทนสมาชิกของเมทริกซ์ A ที่อยู่ในแถวที่ i หลักที่ j เช่น
A = \begin{bmatrix} 2 & 1 & 3 \\ 5 & 0 & 4\end{bmatrix} จะได้ว่า a_{11} = 2, a_{12} = 1, a_{13} = 3, a_{21} = 5, a_{22} = 0, a_{23} = 4
ตัวอย่างที่ 1 กำหนดเมทริกซ์ A = \begin{bmatrix} -1 & 10 & 5 \\ 7 & 9 & 5 \\ 3 & 2 & 1\end{bmatrix} จงหาค่าของ a_{12} + a_{23}
วิธีทำ
a_{12} คือสมาชิกในแถวที่ 1 หลักที่ 2 ทำให้เราได้ว่า a_{12} = 10
a_{23} คือสมาชิกในแถวที่ 2 หลักที่ 3 ทำให้เราได้ว่า a_{23} = 5
ดังนั้นค่าของ a_{12} + a_{23} = 10 + 5 = 15
การเท่ากันของเมทริกซ์
ถ้า A, B เป็นเมทริกซ์ เราจะกล่าวว่า A = B ก็ต่อเมื่อ A กับ B มีขนาดเท่ากันและสมาชิกตำแหน่งเดียวกันต้องมีค่าเท่ากัน หรือง่าย ๆ ก็คือ ถ้าเมทริกซ์จะเท่ากันได้ หน้าตาของมันต้องเหมือนกันเป๊ะ ๆ นั่นเองครับ
ทรานสโพส (Transpose)
คือการเปลี่ยนแถวเป็นหลัก และเราจะใช้ A^t แทนทรานสโพสของเมทริกซ์ A
เช่น A = \begin{bmatrix} 2 & 1 & 3 \\ 5 & 0 & 4\end{bmatrix} เราจะได้ทันทีว่า A^t = \begin{bmatrix} 2 & 5 \\ 1 & 0 \\ 3 & 4\end{bmatrix} นั่นเองครับ
✨พีชคณิตของ เมทริกซ์
เมทริกซ์เอกลักษณ์
ก่อนที่เราจะนำเมทริกซ์มาดำเนินการกันด้วยการบวก การลบ หรือการคูณ เราจำเป็นจะต้องรู้จักเมทริกซ์ชนิดหนึ่งที่มีความสำคัญมากครับ นั่นคือเมทริกซ์เอกลักษณ์
เมทริกซ์เอกลักษณ์คือเมทริกซ์จัตุรัส (แถวและหลักเท่ากัน) ที่มีสมาชิกในแนวเส้นทแยงมุมหลักเป็น 1 และสมาชิกตัวอื่น ๆ ที่เหลือทั้งหมดเป็น 0 และเราจะเขียน I เพื่อแทนเมทริกซ์เอกลักษณ์ เช่น
I_2 = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}, I_3 = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}
การบวก ลบ เมทริกซ์
ถ้า A, B เป็นเมทริกซ์แล้ว A \pm B จะหาค่าได้ ก็ต่อเมื่อ A กับ B มีมิติเท่ากัน และผลลัพธ์ของ A \pm B คือการนำสมาชิกในตำแหน่งเดียวกันมา บวก หรือลบกัน เรามาดูตัวอย่างกันเลยครับ
ตัวอย่างที่ 2 กำหนดเมทริกซ์ A = \begin{bmatrix} -1 & 10 & 5 \\ 7 & 9 & 5 \\ 3 & 2 & 1 \end{bmatrix}, B = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} จงหา A + B
วิธีทำ
\begin{aligned}A + B &= \begin{bmatrix} -1 & 10 & 5 \\ 7 & 9 & 5 \\ 3 & 2 & 1 \end{bmatrix} + \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} \\ &= \begin{bmatrix} -1+1 & 10+2 & 5+3 \\ 7+4 & 9+5 & 5+6 \\ 3+7 & 2+8 & 1+9 \end{bmatrix} \\ &= \begin{bmatrix} 0 & 12 & 8 \\ 11 & 14 & 11 \\ 10 & 10 & 10 \end{bmatrix} \end{aligned}
นั่นคือ A + B = \begin{bmatrix} 0 & 12 & 8 \\ 11 & 14 & 11 \\ 10 & 10 & 10 \end{bmatrix}
นั่นคือ A + B = \begin{bmatrix} 0 & 12 & 8 \\ 11 & 14 & 11 \\ 10 & 10 & 10 \end{bmatrix}
การคูณเมทริกซ์กับสเกลาร์
สำหรับการคูณเมทริกซ์กับสเกลาร์นั้นน้อง ๆ สามารถทำได้อย่างง่ายดายเลยครับ โดยการนำสเกลาร์ไปคูณกับสมาชิกทุกตำแหน่งของเมทริกซ์ เช่น A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \Longrightarrow 2A = \begin{bmatrix} 2 & 0 \\ 0 & 2 \end{bmatrix}
การคูณเมทริกซ์กับเมทริกซ์
สำหรับน้อง ๆ ที่เคยเรียนเรื่องเมทริกซ์มาก่อน ก็คงจะเห็นว่าการคูณเมทริกซ์ด้วยเมทริกซ์นั้นค่อนข้างเข้าใจได้ยาก และชวนให้เราสับสนกว่าการดำเนินการอื่น ๆ ของเมทริกซ์ที่เราได้ทำความเข้าใจไปก่อนหน้านี้ แต่ว่าวันนี้พี่ได้ทำการสรุปมาให้น้องแบบเข้าใจง่าย ๆ ครับ น้อง ๆ สามารถค่อย ๆ อ่านค่อย ๆ ทำความเข้าใจไปพร้อมกันเลยนะครับ ถ้าเข้าใจหลักการแล้ว การคูณเมทริกซ์กับเมทริกซ์นั้น ไม่ได้เป็นเรื่องที่ยากเกินไปแน่นอนน
ถ้า A, B เป็นเมทริกซ์แล้ว AB จะหาค่าได้ ก็ต่อเมื่อ หลักของ A เท่ากับแถวของ B และเมทริกซ์ผลลัพธ์ที่ได้นั้นจะมีขนาดเป็น “แถวของ A \times หลักของ B” และหน้าตาของสมาชิกด้านในเมทริกซ์ผลลัพธ์จะเป็นการนำสมาชิกในแต่ละแถวของ A ไปคูณกับสมาชิกในแต่ละหลักของ B เมื่อรู้แบบนี้แล้ว เราลองไปดูตัวอย่างกันเลยย
ตัวอย่างที่ 3 กำหนดเมทริกซ์ A = \begin{bmatrix} 1 & 3 \\ 2 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} จงหาผลคูณของเมทริกซ์ A และ B
วิธีทำ
A \times B ทำโดยการคูณแถวของเมทริกซ์ A เข้ากับหลักของเมทริกซ์ B โดยเราจะทำได้ดังนี้ครับ
เราจะกำหนดให้เมทริกซ์ผลลัพธ์มีชื่อว่า C
- c_{11} มาจากการคูณแถวที่ 1 ของ A กับหลักที่ 1 ของ B
- (1 \times 5) + (3 \times 7) = 5 + 21 = 26
- c_{12} มาจากการคูณแถวที่ 1 ของ A กับหลักที่ 2 ของ B
- (1 \times 6) + (3 \times 8) = 6 + 24 = 30
- c_{21} มาจากการคูณแถวที่ 2 ของ A กับหลักที่ 1 ของ B
- (2 \times 5) + (4 \times 7) = 10 + 28 = 38
- c_{22} มาจากการคูณแถวที่ 2 ของ A กับหลักที่ 2 ของ B
- (2 \times 6) + (4 \times 8) = 12 + 32 = 44
ดังนั้น ผลคูณของเมทริกซ์ A และ B คือ
A \times B = \begin{bmatrix} 26 & 30 \\ 38 & 44 \end{bmatrix}
✨ดีเทอร์มิแนนต์ของเมทริกซ์
ดีเทอร์มิแนนต์ (Determinant) คือค่าตัวค่าหนึ่งที่เมทริกซ์แต่ละเมทริกซ์จะมีได้เพียงค่าเดียวเท่านั้น โดยเมทริกซ์ที่จะมีดีเทอร์มิแนนต์ได้นั้นจะต้องเป็นเมทริกซ์จัตุรัสเท่านั้น ในหัวข้อนี้พี่จะขออธิบายถึงวิธีการหาค่าของดีเทอร์มิแนนต์ของเมทริกซ์ที่มีขนาด 2 \times 2 และ 3 \times 3
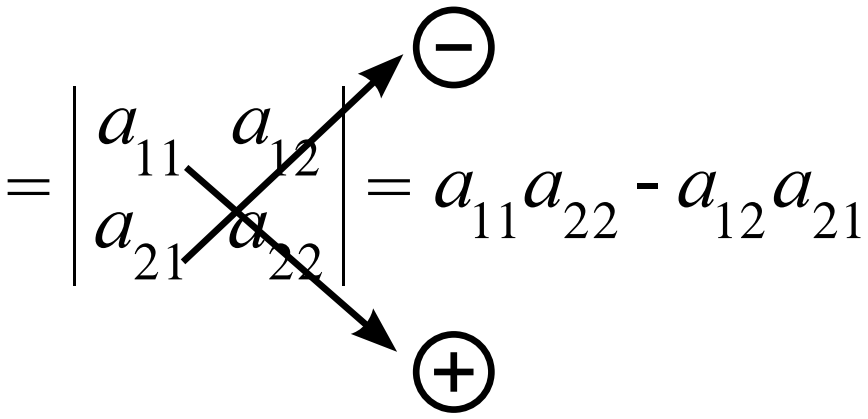
ดีเทอร์มิแนนต์ของเมทริกซ์ที่มีขนาด 2 \times 2
ถ้า A = \begin{bmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \end{bmatrix} แล้ว \operatorname{det}(A) = คูณทแยงล่าง – คูณทแยงบน
ดีเทอร์มิแนนต์ของเมทริกซ์ที่มีขนาด 3 \times 3
ถ้า A = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \end{bmatrix} แล้วเราจะสามารถหา \operatorname{det}(A) ได้โดยการนำหลักที่ 1 และ 2 ไปต่อท้ายกับเมทริกซ์ตั้งต้น แล้วใช้การคูณทแยงเช่นเดิม เพื่อให้เข้าใจมากขึ้น น้อง ๆ สามารถดูรูปนี้ได้เลยครับ
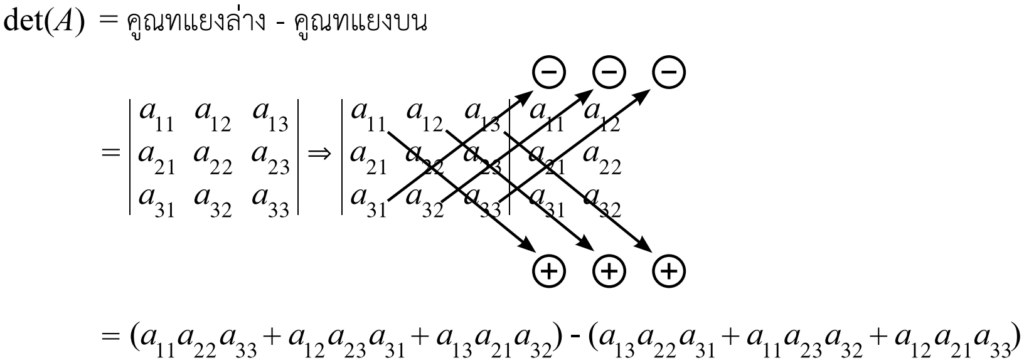
✨สมบัติของดีเทอร์มิแนนต์
- \operatorname{det}(A^t) = \operatorname{det}(A)
- \operatorname{det}(AB) = \operatorname{det}(A)\operatorname{det}(B)
- \operatorname{det}(A^n) = [\operatorname{det}(A)]^n เมื่อ n เป็นจำนวนเต็มบวก
- \operatorname{det}(kA) = k^n \operatorname{det}(A) เมื่อ k เป็นจำนวนจริง และ n เป็นจำนวนแถวหรือหลัก
- \operatorname{det}(I) = 1
- \operatorname{det}(A^{-1}) = [\operatorname{det}(A)]^{-1}
ตัวอย่างที่ 4 กำหนดเมทริกซ์ A = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{bmatrix} จงหาดีเทอร์มิแนนต์ของเมทริกซ์ A
วิธีทำ
- เขียนเมทริกซ์ A แล้วทำการคัดลอกหลักที่ 1 และหลักที่ 2 มาวางต่อท้ายเพื่อให้มีทั้งหมด 5 หลักดังนี้
\begin{bmatrix} 1 & 2 & 3 & 1 & 2 \\ 4 & 5 & 6 & 4 & 5 \\ 7 & 8 & 9 & 7 & 8 \end{bmatrix}
- คำนวณผลคูณของสมาชิกในเส้นทแยงมุมจากซ้ายบนไปขวาล่าง (เส้นทแยงมุมลง) 3 เส้น โดยคูณสมาชิกในแต่ละเส้น แล้วนำมาบวกกัน
- เส้นทแยงมุมแรก: 1 \times 5 \times 9 = 45
- เส้นทแยงมุมที่สอง: 2 \times 6 \times 7 = 84
- เส้นทแยงมุมที่สาม: 3 \times 4 \times 8 = 96
ผลรวมของเส้นทแยงมุมลง: 45 + 84 + 96 = 225
- คำนวณผลคูณของสมาชิกในเส้นทแยงมุมจากซ้ายล่างไปขวาบน (เส้นทแยงมุมขึ้น) 3 เส้น โดยคูณสมาชิกในแต่ละเส้น แล้วนำมาบวกกัน:
- เส้นทแยงมุมแรก: 7 \times 5 \times 3 = 105
- เส้นทแยงมุมที่สอง: 8 \times 6 \times 1 = 48
- เส้นทแยงมุมที่สาม: 9 \times 4 \times 2 = 72
ผลรวมของเส้นทแยงมุมขึ้น: 105 + 48 + 72 = 225
- หาค่าดีเทอร์มิแนนต์โดยนำผลรวมของเส้นทแยงมุมลงลบด้วยผลรวมของเส้นทแยงมุมขึ้น:
\text{det}(A) = 225 – 225 = 0
ดังนั้นดีเทอร์มิแนนต์ของเมทริกซ์ A คือ \text{det}(A) = 0
✨เมทริกซ์ผกผัน
เราจะใช้ A^{-1} แทนเมทริกซ์ผกผันของเมทริกซ์ A โดยที่ A A^{-1} = I = A^{-1} A โดยเมทริกซ์ผกผันนั้น จะนิยามสำหรับเมทริกซ์ที่เป็นเมทริกซ์จัตุรัสเท่านั้น หรือพูดอีกอย่างก็คือ ถ้าไม่ใช่เมทริกซ์จัตุรัส เมทริกซ์นั้นจะไม่มีเมทริกซ์ผกผันนั่นเองครับ
โดยทั่วไปแล้วเราจะมีขั้นตอนวิธีการหาเมทริกซ์ผกผันสำหรับเมทริกซ์จัตุรัสใด ๆ ก็ได้ครับ แต่ในหัวข้อนี้ พี่จะขอแนะนำเพียงแค่วิธีการหาเมทริกซ์ผกผันของเมทริกซ์จัตุรัส 2 \times 2 เท่านั้นครับ
ถ้า A = \begin{bmatrix} a & b \\ c & d \end{bmatrix} แล้ว A^{-1} = \dfrac{1}{\operatorname{det}(A)} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix} จากสูตรน้อง ๆ จะเห็นว่ามี \operatorname{det}(A) อยู่ที่ตัวส่วนด้วย นั่นหมายความว่า ถ้าเมทริกซ์ไหนมี \operatorname{det} เป็น 0 เราจะสรุปว่าเมทริกซ์นั้นไม่มีเมทริกซ์ผกผันนั่นเองครับ
ตัวอย่างที่ 5 กำหนดเมทริกซ์ A = \begin{bmatrix} 2 & 1 \\ 5 & 3 \end{bmatrix}
จงหาว่าเมทริกซ์นี้มีเมทริกซ์ผกผันหรือไม่ หากมี ให้หาเมทริกซ์ผกผันนั้นด้วย
วิธีทำ
จากโจทย์เราจะได้ว่า a = 2, b = 1, c = 5, d = 3
- หาค่าดีเทอร์มิแนนต์ของ A
\operatorname{det}(A) = (a \times d) – (b \times c) = (2 \times 3) – (1 \times 5) = 6 – 5 = 1
เนื่องจากค่าดีเทอร์มิแนนต์ไม่เท่ากับศูนย์ ทำให้เมทริกซ์ A จึงมีเมทริกซ์ผกผัน
- หาเมทริกซ์ผกผันของ A:
A^{-1} = \dfrac{1}{1} \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix} = \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix}
ดังนั้นเมทริกซ์ผกผันคือ A^{-1} = \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix} นั่นเอง
✨ระบบสมการเชิงเส้น
ระบบสมการเชิงเส้น
น้อง ๆ หลายคนอาจจะเคยแก้ระบบสมการเชิงเส้นกันมาแล้วในสมัย ม.ต้น ใช่ไหมครับ ในตอนนั้นเราอาจจะแก้ระบบสมการด้วยวิธีการทำสัมประสิทธิ์ของตัวแปรให้เท่ากัน แล้วค่อย ๆ กำจัดตัวแปรไปเรื่อย ๆ แล้วไล่แทนค่าย้อนกลับจนได้ค่าของตัวแปรครบทุกตัว
ในวันนี้พี่จะแนะนำวิธีการแก้ระบบสมการเชิงเส้นโดยการใช้เมทริกซ์ครับ ซึ่งจะมีอยู่ 2 วิธีด้วยกันดังนี้ครับ
1 การคูณด้วยเมทริกซ์ผกผัน
ถ้าเรามีระบบสมการเชิงเส้น
\begin{aligned} a_1 x + b_1 y &= c_1 \\ a_2 x + b_2 y &= c_2 \end{aligned}
เราจะสามารถเขียนระบบสมการเชิงเส้นนี้ใหม่ในรูปการคูณกันของเมทริกซ์ดังนี้ครับ
\begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix} = \begin{bmatrix} c_1\\ c_2 \end{bmatrix}
และเราจะกำหนดชื่อของเมทริกซ์ดังนี้
A = \begin{bmatrix} a_1 & b_1 \\ a_2 & b_2 \end{bmatrix}, X = \begin{bmatrix} x\\ y \end{bmatrix}, B = \begin{bmatrix} c_1\\ c_2 \end{bmatrix}
ดังนั้นเราสามารถเขียนระบบสมการเชิงเส้นดังกล่าวโดยใช้เมทริกซ์ได้ดังสมการ AX = B นั่นเองครับ
จากสมการ น้อง ๆ จะเห็นได้ว่า สิ่งที่เราต้องการทราบคือเมทริกซ์ X ว่าหน้าตาของมันจริง ๆ แล้วเป็นยังไง ดังนั้นเราจะทำการแก้สมการดังนี้ครับ
\begin{aligned}AX &= B \\ A^{-1}AX &= A^{-1}B \\ IX &= A^{-1}B \\ X &= A^{-1}B\end{aligned}
จากการแก้สมการ เราจะพบว่า ถ้าเราต้องการทราบหน้าตาของเมทริกซ์ X เราจะทำได้โดยการนำ A^{-1} ไปคูณเข้าที่ด้านหน้าของเมทริกซ์ B นั่นเองครับ
2 การใช้เมทริกซ์แต่งเติม
จากวิธีที่ 1 เราสามารถเขียนระบบสมการเชิงเส้นในรูป AX = B ใช่ไหมครับ ในวิธีการนี้ เราจะเขียนสมการดังกล่าวในรูปเมทริกซ์แต่งเติมดังนี้ครับ
AX = B \Longrightarrow [A \mid B]
โดยเป้าหมายของเราคือการใช้การดำเนินการตามแถว (row operation) เพื่อเปลี่ยน [A \mid B] ให้เป็น [I \mid X] นั่นเองครับ ซึ่งการดำเนินการตามแถวที่เราสามารถทำได้นั้น มีอยู่ด้วยกัน 3 ข้อดังนี้ครับ
การดำเนินการตามแถว
- R_i \leftrightarrow R_j : สลับแถวที่ i กับแถวที่ j เช่น
\begin{bmatrix} 1 & 2 &\bigm| & 5 \\ 3 & 4 &\bigm| & 10 \end{bmatrix} \sim \begin{bmatrix} 3 & 4 &\bigm| & 10 \\ 1 & 2 &\bigm| & 5 \end{bmatrix} R_1 \leftrightarrow R_2
- kR_i : นำค่าคงที่ (\neq 0) ไปคูณกับแถวใดแถวหนึ่ง เช่น
\begin{bmatrix} 1 & 2 &\bigm| & 5 \\ 3 & 4 &\bigm| & 10 \end{bmatrix} \sim \begin{bmatrix} 2 & 4 &\bigm| & 10 \\ 3 & 4 &\bigm| & 10 \end{bmatrix} 2R_1
- R_i + kR_j : นำค่าคงที่ (\neq 0) ไปคูณกับแถวใดแถวหนึ่งแล้วนำแถวนั้นไปบวกกับอีกแถว เช่น
\begin{bmatrix} 1 & 2 &\bigm| & 5 \\ 3 & 4 &\bigm| & 10 \end{bmatrix} \sim \begin{bmatrix} 1 & 2 &\bigm| & 5 \\ 5 & 8 &\bigm| & 20 \end{bmatrix} 2R_1 + R_2
เป็นยังไงบ้างครับสำหรับเนื้อหาเรื่องเมทริกซ์ที่พี่นำมาฝากในวันนี้ น้อง ๆ หลายคนอาจจะรู้สึกว่ามีเนื้อหาใหม่ ๆ ที่เราไม่เคยเจอมาก่อนอยู่หลายอย่าง แต่ถ้าน้อง ๆ หมั่นทบทวนและขยันทำโจทย์ เนื้อหาเหล่านี้ก็จะไม่ยากอีกต่อไป และช่วยให้เราเข้าใจ เมทริกซ์ มากขึ้นอย่างแน่นอน ถ้าน้องๆ คิดว่าแค่อ่านบทความแล้วยังไม่พอ พี่ออนดีมานด์มีคอร์สเรียนแนะนำดีๆ มาบอกต่อ
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์