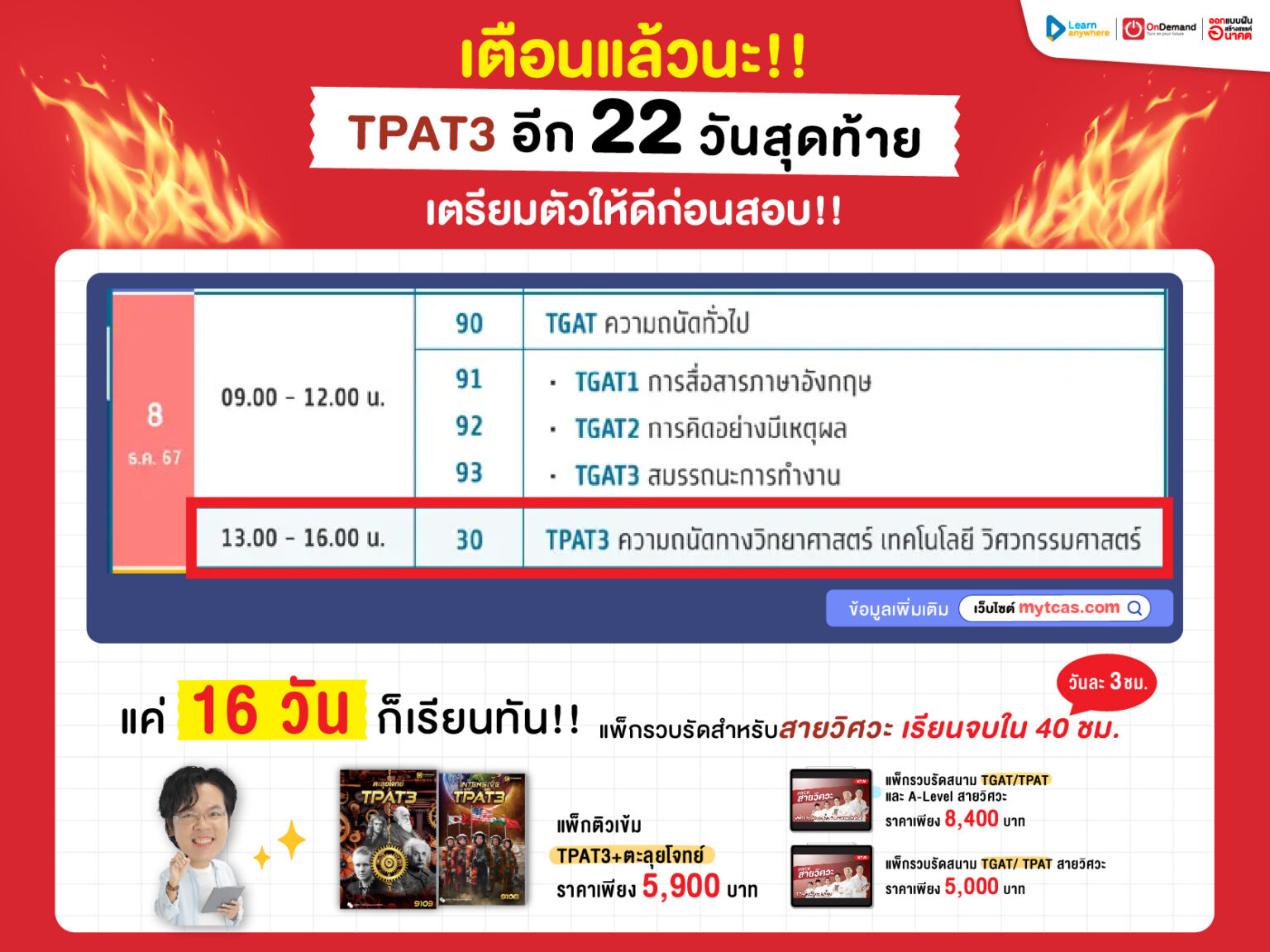
สำหรับน้อง ๆ ม.ปลาย ที่กำลังจะเรียนบทลำดับและอนุกรม วันนี้พี่มีสรุปลำดับและอนุกรมแบบเข้าใจง่าย ๆ มาฝากน้อง ๆ ครับ บทนี้ก็เป็นอีกบทที่มีความสำคัญมากเช่นกัน เพราะบางครั้งโจทย์จากบทอื่นก็จะมีการพูดถึงหรือใช้เนื้อหาจากบทนี้ไปแก้ปัญหาโจทย์ข้อนั้น ๆ ก็ได้ครับ เช่นการนับจำนวนของตัวเลขที่หารด้วยจำนวนเต็มบางอย่างลงตัว เป็นต้น ถ้าน้อง ๆ ทุกคนพร้อมแล้ว ไปลุยกันเลย!
✨ลำดับ คือ อะไร
ลำดับโดยนิยามแล้วหมายถึงฟังก์ชันที่มีโดเมนเป็นเซตของจำนวนเต็มบวก
เช่น f(x) = x^2 เมื่อ x เป็นจำนวนเต็มบวก
x = 1, f(1) = 1 จะเรียก 1 ว่าพจน์ที่ 1 เขียนแทนด้วย a_1 = 1
x = 2, f(2) = 4 จะเรียก 4 ว่าพจน์ที่ 2 เขียนแทนด้วย a_2 = 4
x = 3, f(3) = 9 จะเรียก 9 ว่าพจน์ที่ 3 เขียนแทนด้วย a_3 = 9
x = n, f(n) = n^2 จะเรียก n^2 ว่าพจน์ที่ n เขียนแทนด้วย a_n = n^2
ซึ่งพจน์ที่ n มีอีกชื่อหนึ่งว่า “พจน์ทั่วไป”
✨ชนิดของลำดับ
เราจะแบ่งลำดับออกเป็น 2 ประเภท คือ ลำดับจำกัด และลำดับอนันต์ครับ โดยที่
ลำดับจำกัด คือ ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก n ตัวแรก เขียนแทนด้วย a_1, a_2, a_3, \dots, a_n
ลำดับอนันต์ คือ ลำดับที่มีโดเมนเป็นเซตของจำนวนเต็มบวก เขียนแทนด้วย a_1, a_2, a_3, \dots, a_n, \dots
ต่อไปเราจะไปศึกษาลำดับที่มีคุณสมบัติพิเศษบางอย่างกันครับ โดยจะมีสองลำดับที่เราจะสนใจเป็นพิเศษในระดับ ม.ปลาย นั่นคือ ลำดับเลขคณิต และลำดับเรขาคณิตนั่นเองครับ
✨ลำดับเลขคณิต
คือลำดับที่มีผลต่างของพจน์ที่ n+1 กับพจน์ที่ n เป็นค่าคงที่ และเราจะเรียกค่าคงที่นั้นว่า “ผลต่างร่วม” และจะใช้ d เพื่อแทนผลต่างร่วมครับ
เช่น 2, 4, 6, 8, 10 เป็นลำดับเลขคณิต เพราะว่ามีผลต่างร่วมเท่ากับ 2 นั่นเองครับ (ขวา – ซ้าย มีค่าคงที่)
นอกจากนี้เรายังสามารถเขียนพจน์ทั่วไปของลำดับเลขคณิตได้ด้วยสมการ a_n = a_1 + (n-1)d ครับ
✨ตัวอย่างที่ 1 จงหาพจน์ทั่วไปของลำดับเลขคณิต 2, 4, 6, 8, 10, \dots
✨วิธีทำ
ในการหาพจน์ทั่วไป เราต้องแทนค่าลงในสมการพจน์ทั่วไป นั่นคือสมการ a_n = a_1 + (n-1)d
จะเห็นว่าเราต้องแทนค่าของ a_1 และ d ลงไป ซึ่ง a_1 เราทราบค่าแล้วว่ามีค่าเท่ากับ 2 ต่อไปเราจะหา d หรือผลต่างร่วมกันครับ
d = 4-2 = 6-4 = 8-6 = 10-8 = 2 ดังนั้น d = 2
ดังนั้นทำการแทนค่าจะได้ว่า a_n = 2 + (n-1)2 = 2 + 2n – 2 = 2n
นั่นหมายความว่าพจน์ทั่วไปของลำดับเลขคณิตนี้คือ a_n = 2n นั่นเอง
✨ลำดับเรขาคณิต
คือลำดับที่มีอัตราส่วนของพจน์ที่ n+1 ต่อพจน์ที่ n เป็นค่าคงที่ และเราจะเรียกค่าคงที่นั้นว่า “อัตราส่วนร่วม” และจะใช้ r เพื่อแทนผลต่างร่วม
เช่น 2, 4, 8, 16, 32 เป็นลำดับเรขาคณิต เพราะว่ามีอัตราส่วนร่วมเท่ากับ 2 นั่นเองครับ (ขวา / ซ้าย มีค่าคงที่)
นอกจากนี้เรายังสามารถเขียนพจน์ทั่วไปของลำดับเรขาคณิตได้ด้วยสมการ a_n = a_1(r)^{n-1} ครับ
✨ตัวอย่างที่ 2 จงหาพจน์ทั่วไปของลำดับเรขาคณิต 2, 4, 8, 16, 32, \dots
✨วิธีทำ
ในการหาพจน์ทั่วไป เราต้องแทนค่าลงในสมการพจน์ทั่วไป นั่นคือสมการ a_n = a_1(r)^{n-1}
จะเห็นว่าเราต้องแทนค่าของ a_1 และ r ลงไป ซึ่ง a_1 เราทราบค่าแล้วว่ามีค่าเท่ากับ 2 ต่อไปเราจะหา r หรืออัตราส่วนร่วมกันครับ
r = \dfrac{4}{2}= \dfrac{8}{4} = 2 ดังนั้น r = 2
ดังนั้นทำการแทนค่าจะได้ว่า a_n = 2(2)^{n-1} = 2^n
นั่นหมายความว่าพจน์ทั่วไปของลำดับเรขาคณิตนี้คือ a_n = 2^n นั่นเอง
✨สรุปลำดับเลขคณิตและลำดับเรขาคณิต
✨ลำดับเลขคณิต
ลักษณะพิเศษ : มีผลต่างร่วม d = a_{n+1} – a_n
พจน์ทั่วไป : a_n = a_1 + (n-1)d
✨ลำดับเรขาคณิต
ลักษณะพิเศษ : มีอัตราส่วนร่วม r = \dfrac{r^{n+1}}{r^n}
พจน์ทั่วไป : a_n = a_1(r)^{n-1}
✨ลิมิตของลำดับอนันต์
ถ้าเราให้ a_n เป็นลำดับ เมื่อ n มีค่ามากขึ้นโดยไม่มีที่สิ้นสุดแล้ว a_n มีค่าเข้าใกล้หรือเท่ากับจำนวนจริง L เพียงค่าเดียว เราจะเรียกค่า L ว่าเป็นลิมิตของลำดับ a_n และเขียนเป็นสมการได้ว่า \displaystyle \lim_{n \to \infty} a_n = L และเราจะเรียกลำดับอนันต์นี้ว่าเป็นลำดับลู่เข้า แต่ถ้า \displaystyle \lim_{n \to \infty} a_n ไม่มีลิมิต หรือ หาค่าไม่ได้ เราจะเรียกลำดับเหล่านั้นว่าเป็นลำดับลู่ออก
✨ทฤษฎีลิมิตของลำดับอนันต์
กำหนดให้ a_n, b_n เป็นลำดับของจำนวนจริง และ \displaystyle \lim_{n \to \infty} a_n = A, \lim_{n \to \infty} b_n = B เมื่อ A, B เป็นจำนวนจริง และ c เป็นค่าคงตัวแล้ว เราจะได้ว่า
- \displaystyle \lim_{n \to \infty} c = c
- \displaystyle \lim_{n \to \infty} \dfrac{1}{n^k} = 0 เมื่อ k เป็นจำนวนตรรกยะบวก
- \displaystyle \lim_{n \to \infty} ca_n = c \lim_{n \to \infty} a_n = cA
- \displaystyle \lim_{n \to \infty} (a_n \pm b_n) = \lim_{n \to \infty} a_n \pm \lim_{n \to \infty} b_n = A \pm B
- \displaystyle \lim_{n \to \infty} (a_n \cdot b_n) = \lim_{n \to \infty} a_n \cdot \lim_{n \to \infty} b_n = A \cdot B
- \displaystyle \lim_{n \to \infty} \left(\dfrac{a_n}{b_n}\right) = \dfrac{\lim_{n \to \infty} a_n}{\lim_{n \to \infty} b_n} = \dfrac{A}{B} เมื่อ B \neq 0
- \displaystyle \lim_{n \to \infty} \sqrt[k]{a_n} = \sqrt[k]{\lim_{n \to \infty} a_n} = \sqrt[k]{A} เมื่อ k คือจำนวนเต็มบวก และ \sqrt[k]{A} เป็นจำนวนจริง
เมื่อทราบถึงความหมายและทฤษฎีของลิมิตของดับอนันต์แล้ว ต่อไปเราจะไปลองทำโจทย์กันดูครับ
✨ตัวอย่างที่ 3 กำหนดให้ \displaystyle a_n = \dfrac{7n+2}{n} จงหาค่าของ \displaystyle \lim_{n \to \infty} a_n
✨วิธีทำ
\begin{aligned} \lim_{n \to \infty} a_n &= \lim_{n \to \infty} \left(\dfrac{7n+2}{n}\right) \\&= \lim_{n \to \infty} \left(\dfrac{7n}{n} + \dfrac{2}{n}\right) \\&= \lim_{n \to \infty} \left(7 + \dfrac{2}{n}\right) \\&= \lim_{n \to \infty} 7 + \lim_{n \to \infty} \dfrac{2}{n} \\&= 7 + 0 \\&= 7\end{aligned}
ดังนั้นเราจึงสรุปได้ว่า \displaystyle \lim_{n \to \infty} a_n = 7
✨อนุกรมจำกัด
ถ้า a_1, a_2, a_3, \dots, a_n เป็นลำดับจำกดที่มี n พจน์ เราจะเรียก a_1 + a_2 + a_3 + \dots + a_n ว่าอนุกรม และแทน S_n = a_1 + a_2 + a_3 + \dots + a_n ว่าเป็นผลบวกของอนุกรม
✨อนุกรมเลขคณิต
คือผลบวก n พจน์แรกของลำดับเลขคณิต ซึ่งจะหาได้จาก S_n = \dfrac{n}{2}(a_1 + a_n) หรือ S_n = \dfrac{n}{2}(2a_1 + (n-1)d)
✨ตัวอย่างที่ 4 จงหาค่าของ 1 + 6 + 11 + 16 + \dots + 101
✨วิธีทำ
เนื่องจากอนุกรมนี้เป็นอนุกรมเลขคณิตที่มี d = 5, a_1 = 1, a_n = 101
เราจะหา n ดังนี้
a_n = a_1 + (n-1)d \Longrightarrow 101 = 1 + (n-1)5 \Longrightarrow n-1 = 20 \Longrightarrow n = 21
ดังนั้น 1 + 6 + 11 + 16 + \dots + 101 = S_{21}
ซึ่ง S_{21} = \dfrac{21}{2}(1 + 101) = \dfrac{21 \times 102}{2} = 1071
✨อนุกรมเรขาคณิต
คือผลบวก n พจน์แรกของลำดับเรขาคณิต ซึ่งจะหาได้จาก S_n = \dfrac{a_1(1-r^n)}{1-r} หรือ S_n = \dfrac{a_1(r^n-1)}{r-1} เมื่อ r \neq 1
✨ตัวอย่างที่ 5 จงหาค่าของ 1 + 2 + 4 + 8 + \dots + 512
✨วิธีทำ
เนื่องจากอนุกรมนี้เป็นอนุกรมเรขาคณิตที่มี r = 2, a_1 = 1, a_n = 512
เราจะหา n ดังนี้
a_n = a_1 r^{n-1} \Longrightarrow 512 = 1 (2)^{n-1} \Longrightarrow 2^9 = 2^{n-1} \Longrightarrow n = 10
ดังนั้น 1 + 2 + 4 + 8 + \dots + 512 = S_{10}
ซึ่ง S_{10} = \dfrac{1(2^10-1)}{2-1} = 2^10 – 1 = 1023
✨อนุกรมอนันต์
สำหรับอนุกรมอนันต์นั้นก็เหมือนกันอนุกรมจำกัดเลยครับ คือเป็นการนำพจน์แต่ละพจน์ของลำดับมาบวกเข้าด้วยกัน แต่คราวนี้จะเป็นการบวกไปเรื่อย ๆ ไม่มีที่สิ้นสุด ต่างกับอนุกรมจำกัดที่บวกกันแบบจำกัดพจน์ครับ
โดยอนุกรมอนันต์ที่เราจะศึกษาในระดับ ม.ปลาย นั้นมีเพียงอนุกรมเรขาคณิตอนันต์เท่านั้น การคำนวณจะเป็นยังไง ไปดูกันต่อได้เลยครับ
✨อนุกรมเรขาคณิตอนันต์
เราจะเขียน S_\infty เพื่อแทนอนุกรมเรขาคณิตอนันต์ โดยที่ S_\infty = \dfrac{a_1}{1-r} โดยที่ |r| < 1 นั่นหมายความว่าสำหรับอนุกรมเรขาคณิตอนันต์ใด ๆ เราจะสามารถหาผลบวกมันได้แค่ตัวที่ค่าสัมบูรณ์ของอัตราส่วนร่วมของมันมีค่าน้อยกว่า 1 เท่านั้น ถ้าเป็นค่าอื่นจะไม่สามารถหาค่าได้ครับ เหตุผลที่เป็นแบบนี้ก็เพราะว่าถ้าค่าสัมบูรณ์ของอัตราส่วนร่วมมีค่ามากกว่าหรือเท่ากับ 1 มันจะทำให้ค่าของแต่ละพจน์เพิ่มชึ้นหรือลดลงไปเรื่อย ๆ แบบไม่มีขอบเขตนั่นเองครับ
✨ตัวอย่างที่ 6 จงหาค่าของ 1 + \dfrac{1}{2} + \dfrac{1}{4} + \dots
✨วิธีทำ
เนื่องจากอนุกรมนี้เป็นอนุกรมเรขาคณิตอนันต์ที่มี r = \dfrac{1}{2}, a_1 = 1
ซึ่ง |r| = \left|\dfrac{1}{2}\right| < 1 ดังนั้นอนุกรมเรขาคณิตอนันต์นี้ จะสามารถหาค่าได้ โดยหาได้ดังนี้ครับ
\begin{aligned}1 + \dfrac{1}{2} + \dfrac{1}{4} + \dots &= \dfrac{1}{1-\dfrac{1}{2}} \\&= \dfrac{1}{\dfrac{1}{2}} \\&= 2\end{aligned}
ดังนั้น 1 + \dfrac{1}{2} + \dfrac{1}{4} + \dots = 2
✨อนุกรมรูปแบบพิเศษ
✨อนุกรมผสม
อนุกรมผสมนั้นเป็นอนุกรมที่มีรูปแบบไม่ตายตัว เช่น อนุกรมผสมระหว่างเลขคณิตกับเลขคณิต หรืออนุกรมผสมระหว่างเลขคณิตกับเรขาคณิต เป็นต้น น้อง ๆ สามารถดูวิธีการหาผลบวกได้จากตัวอย่างต่อไปนี้เลยครับ
✨ตัวอย่างที่ 7 จงหาค่าของ \dfrac{3}{2} + \dfrac{5}{2^2} + \dfrac{7}{2^3} + \dots + \dfrac{21}{2^{10}}
✨วิธีทำ
ให้สิ่งที่โจทย์ถามแทนด้วย S
S = \dfrac{3}{2} + \dfrac{5}{2^2} + \dfrac{7}{2^3} + \dots + \dfrac{21}{2^{10}}
สังเกตว่าตัวส่วนเรียงกันเป็นลำดับเรขาคณิตที่ r = \dfrac{1}{2} ดังนั้นเราจะคูณด้วยค่านั้นทั้งสมการ จะได้
\dfrac{1}{2}S = \dfrac{3}{2^2} + \dfrac{5}{2^3} + \dfrac{7}{2^4} + \dots + \dfrac{21}{2^{11}}
นำทั้งสองสมการมาลบกัน จะได้
\begin{aligned}S-\frac{1}{2}S &= \frac{3}{2} + \frac{2}{2^2} + \frac{2}{2^3} + \frac{2}{2^4} + \cdots +\frac{2}{2^{10}} – \frac{21}{2^{11}} \\\dfrac{1}{2}S &= \frac{3}{2} + 2\left(\frac{1}{2^2} + \frac{1}{2^3} + \frac{1}{2^4} + \cdots+ \frac{1}{2^{10}}\right) – \frac{21}{2^{11}} \\&= \frac{3}{2} + 2 \left(\dfrac{\frac{1}{2^2}\left(1-\frac{1}{2^9}\right)}{1-\frac{1}{2}}\right)- \frac{21}{2^{11}} \\&= \frac{3}{2} + 2\left(\dfrac{\frac{1}{2^2} – \frac{1}{2^{11}}}{\frac{1}{2}}\right) -\frac{21}{2^11} \\&= \frac{3}{2} + 4 \left(\frac{1}{2^2} – \frac{1}{2^{11}}\right) – \frac{21}{2^{11}} \\&= \frac{3}{2} + 1 – \frac{4}{2^{11}} – \frac{21}{2^{11}} \\&= \frac{5}{2} – \frac{25}{2^{11}} \\\therefore S &= 5 – \frac{25}{2^{10}}\end{aligned}
เป็นยังไงกันบ้างครับ สำหรับเนื้อหา ลำดับ และ อนุกรม ที่พี่นำมาฝากน้อง ๆ ทุกคนในวันนี้ หลายคนอาจจะยังไม่เข้าใจในครั้งแรกที่อ่าน แต่เราไม่จำเป็นต้องเข้าใจเนื้อหาทั้งหมดนี้ภายในวันเดียวหรือการอ่านเพียงรอบเดียวก็ได้ครับ น้อง ๆ สามารถค่อย ๆ ทบทวนเนื้อหาไปพร้อมกับการฝึกทำโจทย์เพื่อให้เก่งขึ้นได้
ถ้าน้องๆ คิดว่าแค่อ่านบทความแล้วยังไม่พอ พี่ออนดีมานด์มีคอร์สเรียนแนะนำดีๆ มาบอกต่อ
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์

คอร์ส TCAS + ตะลุยโจทย์ คณิต
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand