เมื่อขึ้น ม.ปลาย มา บทแรกในวิชาคณิตศาสตร์ที่น้อง ๆ ส่วนใหญ่จะได้เรียนคือบทเซตนั่นเองครับ สำหรับเนื้อหาในบทเซตนั้นมีความสำคัญกับการเรียนคณิตศาสตร์ในระดับ ม.ปลาย มาก เพราะเป็นเรื่องพื้นฐานที่เราจะใช้ได้หลาย ๆ บทของคณิตศาสตร์ ม.ปลาย เลยครับ เช่น ความสัมพันธ์และฟังก์ชัน จำนวนจริง แคลคูลัส ลำดับและอนุกรม หรือแม้กระทั่งความน่าจะเป็นก็สามารถมีเรื่องเซตไปปนอยู่ได้ด้วยครับ ถ้าพื้นฐานเรื่องเซตเราดี บทอื่น ๆ ก็จะดีตามไปด้วยครับ
วันนี้พี่ก็ได้เตรียมสรุปเนื้อหาเรื่องเซตแบบเน้น ๆ มาให้น้อง ๆ ได้อ่านกันครับ โดยเนื้อหาก็จะประกอบด้วยพื้นฐานเรื่องเซตทั้งหมด สับเซต เพาเวอร์เซต แผนภาพเวนน์และออยเลอร์ การดำเนินการของเซต พร้อมกับตัวอย่างโจทย์ให้น้อง ๆ ได้ฝึกทำกันด้วยครับ ถ้าพร้อมแล้วไปดูเนื้อหากันเลยครับบ
✨ความรู้พื้นฐานของ เซต
การเขียนเซต
เราจะสามารถเขียนได้ 2 แบบ ดังนี้ครับ
- แบบแจกแจงสมาชิก
ทำได้โดยการเขียนสมาชิกทุกตัวลงใน \{ \, \} และใช้เครื่องหมาย \, , คั่นระหว่างสมาชิกแต่ละตัว
เช่น ให้ A แทนเซตของจำนวนเต็มที่มีค่ามากกว่า 7 แต่ไม่เกิน 10 เราจะสามารถเขียนเซต A แบบแจกแจงสมาชิกได้ว่า A = \{8, 9, 10\} นั่นเองครับ
ต่อไป เราจะไปดูการเขียนเซตแบบบอกเงื่อนไขกันครับ แต่ก่อนที่จะไปที่เนื้อหา น้อง ๆ ต้องรู้จักสัญลักษณ์เหล่านี้ก่อน
\mathbb{R} แทนเซตของจำนวนจริง
\mathbb{I}, \mathbb{Z} แทนเซตของจำนวนเต็ม
\mathbb{N} แทนเซตของจำนวนนับ
\in แทนคำว่า เป็นสมาชิกของ
\notin แทนคำว่า ไม่เป็นสมาชิกของ
n(A) แทนจำนวนสมาชิกของเซต A
2. แบบบอกเงื่อนไข
เราจะใช้ตัวอักษรภาษาอังกฤษตัวพิมพ์เล็ก x แทนสมาชิกของเซต แล้วบรรยายสมบัติของสมาชิกหลังเครื่องหมาย \mid (อ่านว่า โดยที่ ซึ่ง) และต้องมีการกำหนดสิ่งที่เราสนใจซึ่งเรียกว่า เอกภพสัมพัทธ์ (U) ด้วยครัล
เช่น ให้ A แทนเซตของจำนวนเต็มที่มีค่ามากกว่า 7 แต่ไม่เกิน 10 เราจะสามารถเขียนเซต A แบบบอกเงื่อนไขได้ว่า A = \{x \in \mathbb{Z} \mid 7 < x \leqslant 10\} นั่นเองครับ
ข้อควรระวัง ไม่จำเป็นที่เซตแต่ละเซตสามารถเขียนเป็นเซตแบบบอกเงื่อนไขได้แบบเดียว
✨ชนิดของเซต
เซตจำกัด
คือเซตที่สามารถบอกจำนวนสมาชิกได้ เช่น ถ้า A = \{8, 9, 10\} เราจะได้ว่า n(A) = 3
เซตอนันต์
คือเซตที่ไม่สามารถบอกจำนวนสมาชิกได้ (เพราะมีสมาชิกอยู่มากมายนับไม่ถ้วน) เช่น A คือเซตของจำนวนจริงที่มีค่ามากกว่า 0 แต่น้อยกว่า 1
เซตว่าง
คือเซตที่มีจำนวนสมาชิกเป็น 0 และเราจะใช้ \{\} หรือ \varnothing แทนเซตว่าง
✨เซตที่เท่ากัน
A = B ก็ต่อเมื่อ เซตทั้งสองมีสมาชิกเหมือนกันทุกตัว
เช่น \{1, 2, 3, 4, 5\} = \{5, 4, 3, 2, 1\} เป็นต้น
✨สับเซต
A เป็นสับเซตของ B ก็ต่อเมื่อ สมาชิกทุกตัวของ A เป็นสมาชิกของ B และเราจะใช้สัญลักษณ์ A \subset B แทน A เป็นสับเซตของ B
ข้อตกลง : เซตว่างเป็นสับเซตของทุกเซต
✨ตัวอย่างที่ 1 จงหาสับเซตทั้งหมดของ A = \{1, 2\}
จากความหมายของสับเซต เราจะได้ว่า \varnothing, \{1\}, \{2\}, \{1, 2\} เป็นสับเซตของ A = \{1, 2\}
จาก✨ ตัวอย่างที่ 1 เราจะพบสิ่งที่น่าสนใจดังนี้ครับ
- A จะเป็นสับเซตของ A เสมอ
- จำนวนสับเซตของ A ทั้งหมดที่เป็นไปได้จะสามารถหาได้จาก 2^{n(A)}
✨เพาเวอร์เซต
เพาเวอร์เซตของ A คือ เซตของสับเซตทั้งหมดของ A หรือพูดง่าย ๆ ก็คือ ให้น้องไปหาสับเซตของ A มาก่อนว่ามีอะไรบ้าง แล้วให้น้องเอาสับเซตพวกนั้นมาเขียนรวมกันไว้ในเซต ๆ เดียว เราจะเรียกเซตนั้นว่าเพาเวอร์เซตของ A นั่นเองครับ และเราจะใช้ P(A) แทนเพาเวอร์เซตของ A ครับ
✨ตัวอย่างที่ 2 จงหาเพาเวอร์เซตของ A = \{1, 2\}
จากความหมายของสับเซต เราจะได้ว่า \varnothing, \{1\}, \{2\}, \{1, 2\} เป็นสับเซตของ A = \{1, 2\} ดังนั้นเราเลยจะได้ว่า P(A) = \{\varnothing, \{1\}, \{2\}, \{1, 2\}\}
จาก✨ ตัวอย่างที่ 2 เราจะพบสิ่งที่น่าสนใจดังนี้ครับ
- A จะเป็นสมาชิกของ P(A) เสมอ
\varnothing จะเป็นสมาชิกของ P(A) เสมอ
✨แผนภาพเวนน์-ออยเลอร์
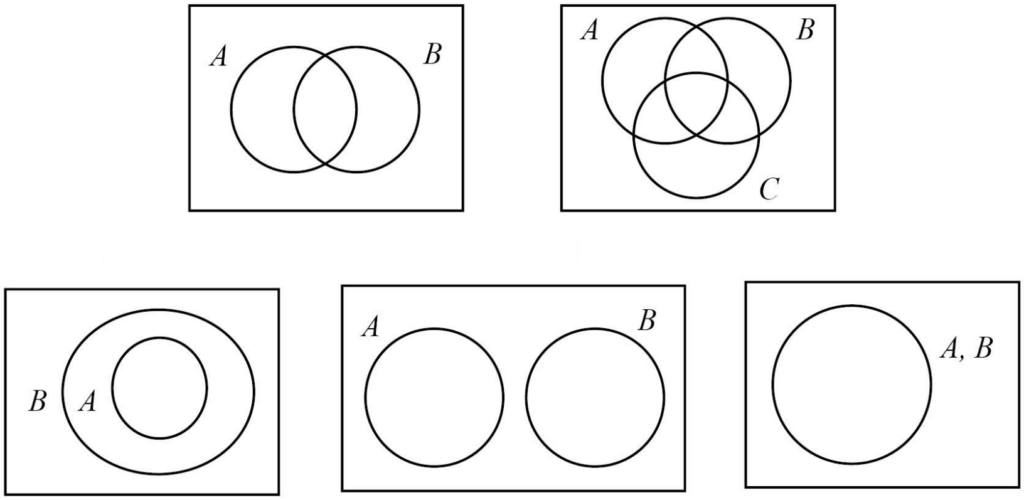
แผนภาพเวนน์-ออยเลอร์ คือการที่เราเขียนแสดงเซตในรูปแบบของแผนภาพ โดยเรามักจะวาดเซตเป็นวงกลมอยู่ภายในกล่องสี่เหลี่ยมที่เป็นเอกภพสัมพัทธ์ครับ และต่อไปนี้คือตัวอย่างของแผนภาพเวนน์-ออยเลอร์ที่น้อง ๆ จะได้เจอบ่อย ๆ เมื่อเรียนเรื่องนี้นั่นเองครับ
✨การดำเนินการของเซต
การดำเนินการของเซตก็คล้าย ๆ กับการบวกลบเลขทั่วไปเลยครับ แต่เป็นในรูปแบบและมุมมองของเซตแทนที่จะเป็นตัวเลข การดำเนินการของเซตที่น้อง ๆ ต้องรู้จักจะมีอยู่ทั้งหมด 4 อย่างคือ ยูเนียน อินเตอร์เซคชัน ผลต่าง คอมพลีเมนต์ครับ

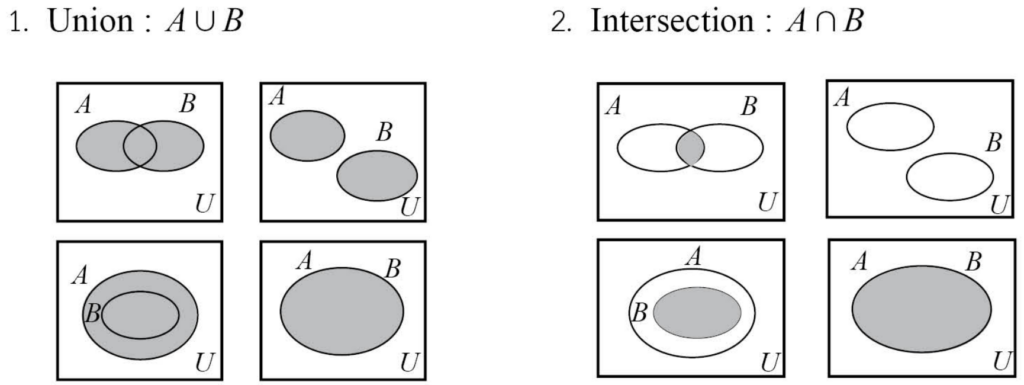
แผนภาพเวนน์-ออยเลอร์ กับการดำเนินการของเซต
เมื่อเรานำความรู้เรื่องแผนภาพเวนน์-ออยเลอร์ มาใช้กับการดำเนินการของเซต แผนภาพที่เราได้ จะเป็นแบบนี้ครับ
✨ตัวอย่างที่ 3 กำหนดให้ U = \{0, 1, 2, 3, 4\}, A = \{0, 1, 3\}, B = \{1, 2, 3\} จงหา A \cup B, A \cap B, A-B
จากความรู้เรื่องการดำเนินการของเซต เราจะได้ว่า
A \cup B = \{0, 1, 2, 3\}
A \cap B = \{1, 3\}
A – B = \{0\}
✨ตัวอย่างที่ 4 กำหนดให้ U = \{0, 1, 2, 3, 4\}, A = \{0, 1, 3\}, B = \{1, 2, 3\} จงหา B-A, A’, B’
จากความรู้เรื่องการดำเนินการของเซต เราจะได้ว่า
B-A = \{2\}
A’ = \{2, 4\}
B’ = \{0, 4\}
สมบัติของการดำเนินการของเซต
- A \cup B = B \cup A
- A \cap B = B \cap A
- A \cup (B \cap C) = (A \cup B) \cap (A \cup C)
- A \cap (B \cup C) = (A \cap B) \cup (A \cap C)
- (A \cup B)’ = A’ \cap B’
- (A \cap B)’ = A’ \cup B’
- A-B = A \cap B’
- A’ = U – A เมื่อ U คือเอกภพสัมพัทธ์
✨การใช้แผนภาพเวนน์-ออยเลอร์ในการแก้โจทย์ปัญหา
ในหัวข้อนี้เราจะนำความรู้เรื่องแผนภาพเวนน์-ออยเลอร์ กับการดำเนินการของเซตมาใช้ควบคู่กันเพื่อแก้ปัญหาต่าง ๆ ในชีวิตประจำวันที่เกี่ยวข้องกับเซตครับ โดยโจทย์ในหัวข้อนี้นั้นส่วนใหญ่จะเป็นการคิดเกี่ยวกับเซตสองหรือสามเซต ดังนั้นแผนภาพเวนน์-ออยเลอร์ที่น้อง ๆ จะต้องวาดขึ้นมาแทบจะทุกข้อเลยก็คือสองรูปต่อไปนี้ครับ
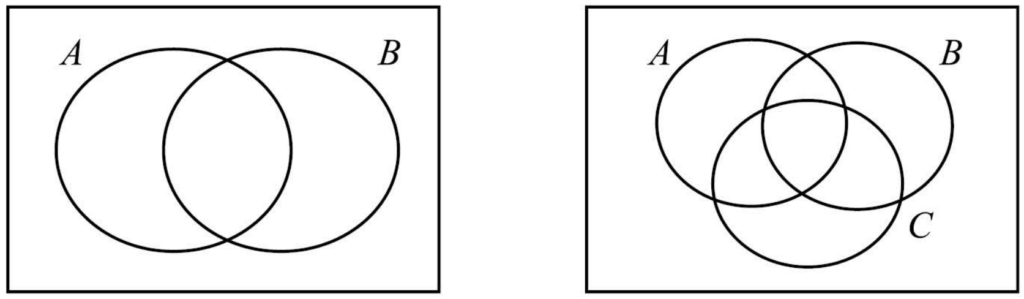
นอกจากแผนภาพข้างต้นแล้ว น้อง ๆ จะต้องรู้สูตรในการคำนวณด้วยครับ โดยสูตรที่เราควรรู้ก็จะมีดังนี้เลยยย
สูตรที่ควรรู้
- n(A \cup B)=n(A)+n(B)-n(A \cap B)
- n(A \cup B \cup C)=n(A)+n(B)+n(C)-n(A \cap B)-n(A \cap C)-n(B \cap C) + n(A \cap B \cap C)
- n(A-B)=n(A)-n(A \cap B)=n(A \cup B)-n(B)
- n(A’)=n(U)-n(A)
✨ตัวอย่างที่ 5 จากการสอบถามนักเรียนชั้น ม.4 มีนักเรียนที่ชอบดื่มน้ำส้มหรือน้ำมะนาวอยู่ทั้งหมด 150 คน ถ้ามีนักเรียนที่ชอบดื่มน้ำส้ม 80 คน ชอบดื่มน้ำมะนาว 90 คน แล้วมีนักเรียนกี่คนที่ชอบดื่มน้ำส้มและน้ำมะนาว
ให้นักเรียนที่ชอบดื่มน้ำส้มแทนด้วยเซต A
ให้นักเรียนที่ชอบดื่มน้ำมะนาวแทนด้วยเซต B
จากสูตร เราจะได้ว่า
n(A \cup B) = n(A) + n(B) – n(A \cap B)
150 = 80 + 90 – n(A \cap B)
150 = 170 – n(A \cap B)
n(A \cap B) = 20
เราจึงสรุปได้ว่ามีนักเรียนที่ชอบดื่มน้ำส้มและน้ำมะนาว 20 คน
เป็นยังไงกันบ้างครับน้อง ๆ สำหรับสรุปเนื้อหาเรื่องเซตที่พี่ได้นำมาฝากในวันนี้ มีทั้งความรู้พื้นฐานของเซต การจำแนกประเภทของเซต สับเซต การใช้สูตร การใช้แผนภาพ เรื่องเหล่านี้น้อง ๆ จะได้ใช้จริงในโรงเรียนและใช้ในการสอบเข้ามหาวิทยาลัยด้วยครับ หากน้อง ๆ อ่านแล้วยังรู้สึกว่าไม่เข้าใจ ให้เราลองวาดแผนภาพประกอบไปด้วย จะทำให้เราเข้าใจเรื่องเซตได้ดีมากขึ้นครับ แล้วก็อย่าลืมทบทวนเนื้อหาบ่อย ๆ ด้วยนะครับบ
บทความอื่นๆ เพิ่มเติม 👉 : OnDemand
คอร์สเรียนแนะนำ
โดยพี่ออนดีมานด์